Объяснение:
ΔABC подібний ΔA₁B₁C₁ ; P : P₁ = 2 : 5 ; якщо а і а₁ - найменші сторони ,
то а + а₁ = 28 см ; а₁ = 28 - а .
Як відомо a / a₁ = P/P₁ ; a /( 28 - a ) = 2/5 ;
5a = 56 - 2a ;
5a + 2a = 56 ;
7a = 56 ;
a = 8 см ; а₁ = 28 - 8 = 20 ( см ) .
За умовою a : b : c = 4 : 5 : 6 ; a = 8 = 4m ; m = 8 : 4 = 2 , тоді
b = 5m = 5*2 = 10 ( см ) ; с = 6m = 6*2 = 12 ( см ).
ΔАВС : 8 см , 10 см , 12 см .
Аналогічно a₁ : b₁ : c₁ = 4 : 5 : 6 ; a₁ = 20 = 4n ; n = 20 : 4 ; n = 5 , тоді
b₁ = 5n = 5*5 = 25 ( см ) ; c₁ = 6n = 6*5 = 30 ( см ) .
ΔА₁В₁С₁ : 20 см , 25 см , 30 см .
Задача 6
В ΔАВС , АВ=ВС, АЕ -биссектриса, Е∈ВС. Найти Р( АВС), если ВС-АС=8 и ВЕ:ЕС=3:2.
Решение.
Пусть одна часть х. Тогда ВЕ=3х, ЕС=2х ⇒ ВС=5х ⇒ АВ=5х , т.к треугольник равнобедренный.
По т. о биссектрисе треугольника
, тогда 
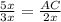⇒ AC=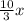
.
По условию ВС-АС=8 , поэтому 5х-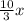
= 8 или 
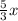=8 или х=4,8.
ВС=5*4,8=24 , АВ=24 , АС=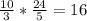
.
Р=24+24+16=64.
Задача 8
Стороны треугольника относятся как 2:3:3 . Найти периметр треугольника , если основание на 5 единиц меньше боковой стороны.
Решение .
Дан ΔАВС. АВ=ВС . Пусть одна часть х. Тогда АВ=ВС=3х, АС=2х .
По условию АС меньше АВ на 5, т.е АВ-АС=5.
Получим 3х-2х=5 или х=5 . Тогда АВ=ВС=3*5=15, АС=2*5=10 .
Р=15+15+10=40.
Задача 9
Угол при вершине равнобедренного треугольника равен 120°. , высота , опущенная на основание, равна 6 .Найти периметр треугольника .
Решение .
Дан ΔАВС , АВ=ВС ,ВН⊥АС , ∠АВС=120°.
1) Высота равнобедренного треугольника является биссектрисой ⇒∠АВН=60° .
2) ΔАВН -прямоугольный , по свойству углов ∠А=90°-60°=30°.
Против угла в 30° , лежит катет равный половине гипотенузы , т.е ВН=1/2*АВ ⇒ АВ=12 ⇒ВС=12, т.к треугольник равнобедренный.
По т. Пифагора АН²=АВ²-ВН² или АН²=12²-6² или АН=√18*6=6√3.
3) Высота равнобедренного ΔАВС является медианой, значит АН=НС=6√3 ⇒АС =12√3.
4)Р=12√3+12+12=24+12√3.