Расстояние от точки до плоскости -- это длина перпендикуляра , опущенного из этой точки на плоскость. ⇒
ВС - перпендикуляр, и треугольник АВС - прямоугольный. Так как все точки одной из параллельных плоскостей находятся на одинаковом расстоянии от другой плоскости, то АА₁=ВС, и прямоугольные треугольники АВА₁ и АВС равны, т.к. у них общая гипотенуза и по равному катету. ⇒ АС=А₁В.
Определение: Проекция точки на плоскость -- это основание перпендикуляра, опущенного из этой точки на плоскость. Множество проекций точек прямой на плоскость образуют проекцию этой прямой.⇒ А₁В и АС- проекции отрезка АВ на каждую из плоскостей.
Стороны треугольника АВС составляют одну из Пифагоровых троек, где стороны прямоугольного треугольника - целые числа. В этой тройке больший катет равен 12 ( можно проверить по т. Пифагора).
Проекции отрезка АВ на параллельные плоскости равны. АС=А₁В=12
-----
2.
Расстояние от точки до плоскости -- это длина перпендикуляра , опущенного из этой точки на плоскость. Следовательно, углы ВВ₁А=СС₁А=90°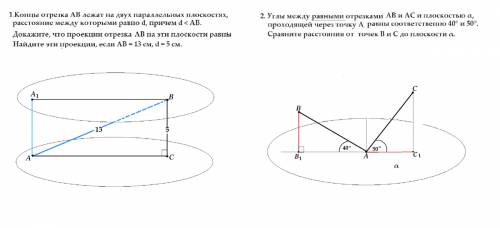
Параллельные прямые СС₁ и ВВ₁ задают плоскость β, которая пересекается с плоскостью α по прямой В₁С₁.
Точки В и С отрезка АВ лежат в этой плоскости, значит весь отрезок АВ лежит в плоскости β.
Итак, точки А, В₁ и С₁ лежат в плоскости β и лежат в плоскости α, значит они принадлежат одной прямой - линии пересечения плоскостей α и β.