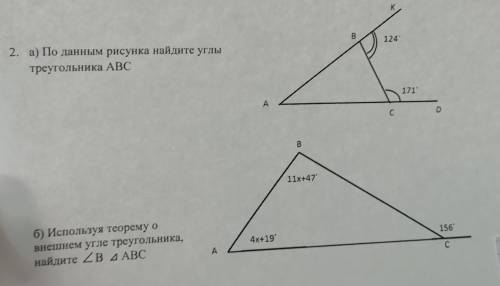
2.а)АВС=56°
АСВ=9°
ВАС=115°
б)АСВ=24°
АВС=43°
ВАС=113°
а)КВС+АВС=180°
АВС=180°-КВС=180°-124°=56°
ВСD+ACB=180°
ACB=180°-BCD=180°-171°=9°
сумма углов треугольника равна 180° поэтому:
ВАС=180°- (АВС+АСВ)=180°- (56°+9°)=115°
б)АСВ+156°=180°
АСВ=180°-156°=24°
сумма углов треугольника равна 180° поэтому:
180°= АВС+ВАС+АСВ= 4х+19°+11х+47°+24°
180°-19°-47°-24°=4х+11х
90°=15х
х=6
ВАС=11х+47°= 11 * 6° +47°= 113°
АВС=4х+19°= 4* 6° +19°= 43°
Можно найти площадь методом нахождения площади всех фигур, при этом прибавив их
Площадь прямоугольника с сторонами 5 и 1 = 5 ед.²
Опустим высоту с стороны прямоугольника длиной 1 ед. Она будет равняться 2, так как высота будет параллельна с высотой слева. У нас получился ещё один прямоугольник с сторонами 5 и 2. Его площадь равна 10 ед.² (если что, для площади прямоугольника мы умножаем стороны)
У нас также появился треугольник с сторонами 2 и (9-5) = 4. Найдём площадь данного треугольника: 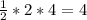 ед.²
ед.²
Треугольник слева будет равен треугольнику, который мы создали, так что его площади тоже равна 4 ед.²
Прибавляем все значения. Это равняется 23 ед.²
∠KBC и ∠ABC - смежные ⇒ ∠KBC+∠ABC=180°⇒
124°+∠ABC=180°
∠ABC=180°-124°
∠ABC=56°
∠CDB и ∠ACB - смежные ⇒ ∠CDB+ ∠ACB=180°⇒
171°+∠ACB=180°
∠ACB=180°-171°
∠ACB=9°
∠BAC=115° так как сумма всех углов треугольника равна 180°⇒
180°-56°-9°=115°
Объяснение:
не уверена в правильности