Я немного поправлю предыдущего товарища :))) хотя в общем случае его решение правильное, но в условии все-таки сказано, что боковые стороны равны меньшему основанию, поэтому "предельным снизу" случаем является квадрат, то есть минимальное отношение оснований (отношние большего основания к меньшему, это у предыдущего товарища тоже опечатка) равно 1 (максимальное, само собой, равно 3, когда трапеция "вытягивается" в отрезок). Если отношение оснований меньше 1, то боковые стороны будут равны большему из оснований, а это противоречит условию :)))
На самом деле - это крохоборство :
1)из ∆DOC найдём угол С :
С=180-(90+70)=20,
2) в ∆ABD Угол D=180-(90+50)=40,
Отсюда угол ADO=90-40=50,
3) Угол AOD и DOC смежные, тогда угол AOD=180-70=110,
4) из ∆ADO, угол A=180-(110+50)=20,
5)в ∆ EDC угол С=180-(90+45)=45,
6) в ∆ADC угол CAD=DCA, значит треугольник равнобедренный,AD=DC,
7) в ∆EDC угол DEC=DCE, значит треугольник равнобедренный, ED=DC,
Следовательно AD=ED, тогда треугольник ADE равнобедренный, а у равнобедренного треугольника углы при основании ровны,
Тогда из ∆ADE : угол А=Е : Тогда (180-50)/2=65.
ответ:65.
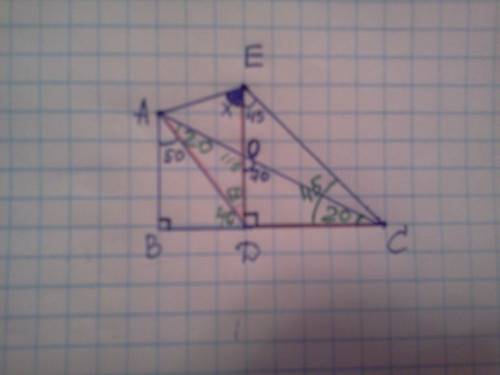
Объяснение:
ну там вот-так, чертить не стал, долго будет, надеюсь почерк понятный