Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис.2).
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1 (см. рис.2). Докажем, что Δ ABC = Δ A1B1C1.
Так как ∠ А = ∠ А1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.
Теорема 2. Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 34).
Замечание. На основе теоремы 2 устанавливается теорема 3.
Теорема 3. Сумма любых двух внутренних углов треугольника меньше 180°.
Из последней теоремы вытекает теорема 4.
Теорема 4. Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Объяснение:
1) Получившийся треугольник авн равнобедренный( тк один угол прямой и бессиктрисса прямого угла проведена те 45, то есть в авн углы при основании равны - признак равнобедренного треугольника) отсюда ав=ан=5 , вс=5+5=10 В прямоугольнике проивоположные стороны равны -1св-во) отсюда P=10*2+5*2=20+10=30см
ответ 30см
2)P=4а, где а сторона ромба. Можно вычислить сторону: 8корней из 3/4 =2корня из 3
Ромб состоит из двух равных треугольников (равны по 3 признаку-3сторонам) Можно найти площадь ромба как сумму площадей двух треугольников
s=1/2 а а sin угла 1/2 * 2корня из 3 на 2корня из 3 на корень из 3 на 2 ( синус 60 корень из трех на два) ( Площадь вычислили по формуле площадь треугольника равна одной второй произведению сторон на синус угла между ними) S=3 на корень из 3 =) s ромба 2*3 корень из 3 = 6 корней из 3
cosC=0,866
<C=30 градусов
Объяснение:
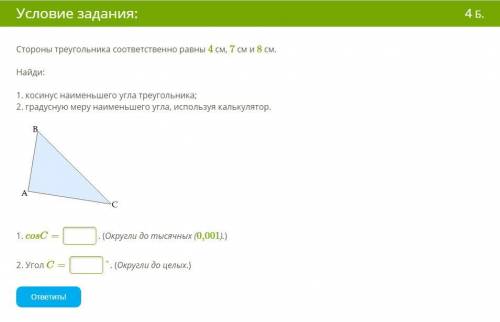
Против меньшей стороны лежит меньший угол :
АВ<АС<ВС
4<7<8
С<В<А
Из теоремы косинусов :
cosC=(AC^2+BC^2-AB^2)/2×AC×BC=
=(7^2+8^2-4^2)/2×7×8=
=(49+64-16)/112=97/112=0,866
<C=29,9947=30 градусов