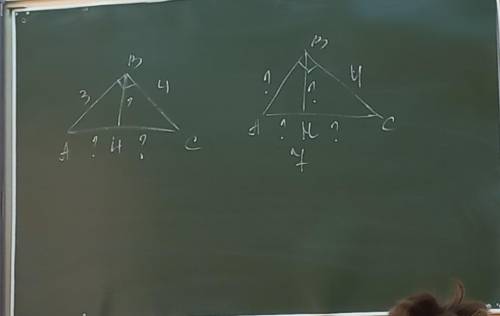
Объяснение:
1) Так как искомый центр гомотетии лежит на одной прямой с точками Х и X', то для нахождения центра проведем прямую XX'.
Условия заданий приводятся в учебных целях и в необходимом объеме — как иллюстративный материал. Имя автора и название цитируемого издания указаны на титульном листе данной книги. (Ст. 19 п. 2 Закона РФ об авторском праве и смежных правах от 9 июня 1993 г.)
2) Так как N = 2, то по определению гомотетии ОХ' = 20Х, где О — центр гомотетии, значит, отложим от точки X' отрезок ОХ' = 2ОХ и получим искомую точку О.
Т.к. треугольник АВС равнобедренный, то высота, проведенная из его вершины к основанию, является ещё его биссектрисой и медианой ( свойство равнобедренного треугольника).
Тогда медианы ВН и АМ пересекающиеся в точке О, делятся этой точкой в отношении 2:1, считая от вершин (свойство медиан).
Медиана АМ делится на АО=30 (2/3 от 45), и ОМ=15( 1/3 от 45).
В прямоугольном треугольнике АОН катет ОН противолежит углу 30° и равен половине гипотенузы АО.
ОН=30•sin30ª=15
ОН по свойству медианы равен одной третьей ВН.
Отсюда ВН=3•ОН=45.