Відповідь:
3 см
Пояснення:
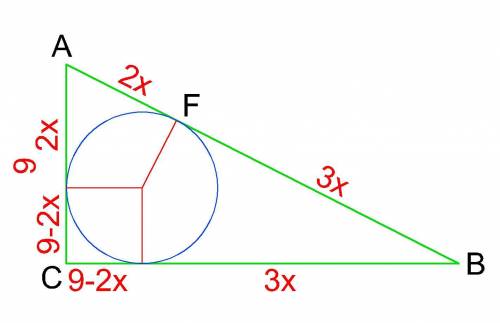
Відомо, що коло, вписане в трикутник, точками дотику до сторін відділяє рівні відрізки зі сторони кожної вершини.
Також відомо, що висоти - радіуси, проведені із центра такого кола в прямокутному трикутнику до катетів утворюють з відрізками від точок дотику до вершини прямого кута квадрат зі стороною, рівною радіусу вписаного кола.
Згідно з умовою, позначимо AF як 2x, FB як 3x, тоді
r=9-2x
За теоремою Піфагора складемо рівняння:
9²+ (9-2х+3х)²=(2х+3х)²
81+(9+х)²=25х²
81+81+18х+х²-25х²=0
24х²-18х-162=0
4х²-3х-27=0
Дискрімінант: Д=9+4*4*27=441=21²
х₁=(3+21)/8=3 см
х₂=(3-21)/8=-2.25 см (не підходить).
Тоді r=9-2·3=3 см
Две прямые касаются окружности (радиусом 9 см) с центром О в точках Р и K и пересекаются в точке M. Найдите угол между этими прямыми, если ОМ = 18 см.
Объяснение:
Дано Окр О( R=9) , МР, МК-касательные , ОМ=18 см.
Найти ∠РМК.
Решение.
ΔРМО-прямоугольный, по свойству касательной. Т.к гипотенуза ОМ = 18 см, катет ОР =9 см в два раза меньше , то угол ∠РМО=30°.
Отрезки касательных к окружности, проведенных из одной точки М, равны и составляют равные углы ( это ∠РМО и ∠КМО ) с прямой, проходящей через эту точку и центр окружности ⇒∠РМО и ∠КМО.
Тогда ∠РМК=∠РМО + ∠КМО= 30°+30°=60°
ответ.∠РМК=60°
S(пп) = 122 см²
Объяснение:
Дано:
a = 4 cm
c = 3 cm
Площадь боковой поверхности: S(бп) = 66 cm²
Найти:
Площадь полной поверхности: S(пп) = ?
Для начала найдём вторую сторону основания b:
Для этого воспользуемся формулой:
S(бп) = P(осн)*с, где P(осн) - периметр основания = 2(a+b), ⇒
S(бп) = 2(a+b)*c
подставим имеющиеся значения:
66 = 2(4+b)*3
66 = 6(4+b)
66 = 24 + 6b
6b = 66-24
6b = 42
b = 42/6
b = 7 см
Площадь полной поверхности прямоугольного параллелепипеда S(пп) определяется по формуле:
S(пп) = 2(ab+bc+ac)
подставим имеющиеся значения:
S(пп) = 2(4*7 + 7*3 + 4*3)
S(пп) = 2(28+21+12)
S(пп) = 2*61
S(пп) = 122 см²