Объяснение:
Дано:
Δ ABC - равнобедренный.
AB = CB; CB - ?° в 3 раза больше основания AC.
P Δ ABC = 133 см.
Найти:
AB; CB; AC.
Пусть x (см) равно основание AC, тогда боковая сторона CB равна 3x (см). Так как в равнобедренном тр-ке боковые стороны равны, то CB = AB = 3x (см). Периметр данного равнобедренного тр-ка равен 133 (см).
Составление математической модели:
3x (см) + 3x (см) + x (см) = 133 (см)
Работа с математической моделью:
6x + x = 133
7x = 133
x = 133 : 7
ответ математической модели:
x = 19
19 (см) равно основание AC.
1) 3x = 3 * 19 = 57 (см) равна боковая сторона CB.
т.к. в равнобедренном треугольнике боковые стороны равны, то ⇒ AB = CB = 57 (см).
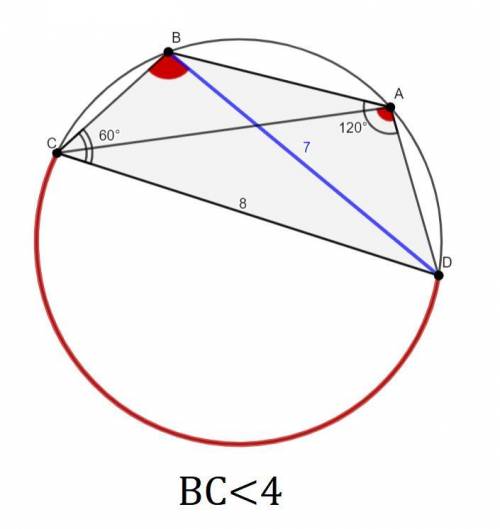
∠BAD+∠BCD = 180°;
∠BCA = 180°-∠BAD = 180°-120° = 60°
Вписанные углы опирающиеся на одну дугу равны.∠CAD - вписанный и опирается на ∪CD
∠CBD - вписанный и опирается на ∪CD
∠CAD = ∠CBD
По теореме синусов в треугольнике CBD: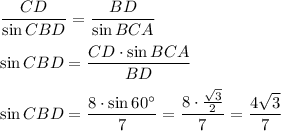
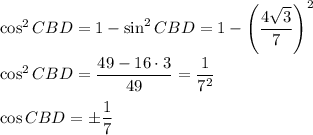
Пусть BC=x, тогда 0<x<4.
Рассмотрим случай, когда cos(CBD) = 1/7По теореме косинусов в треугольнике CBD:
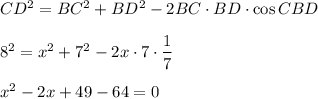
x²-2x-15 = 0
D = (-2)²-4·1·(-15) = 4+60 = 8²
x₁ = (2+8)/2 = 10/2 = 5
x₂ = (2-8)/2 = -6/2 = -3
Ни один корень не подходит под условие 0<x<4.
Теперь случай, когда cos(CBD) = -1/7По теореме косинусов в треугольнике CBD:
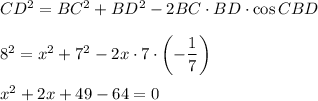
x²+2x-15 = 0
D = 2²-4·1·(-15) = 4+60 = 8²
x₃ = (-2+8)/2 = 6/2 = 3
x₄ = (-2-8)/2 = -10/2 = -5
0 < x₃ < 4
x = 3 удовлетворяет условию, значит cos(CBD) = -1/7.
cos(CBD) < 0, а sin(CBD) > 0. Поэтому ∠CBD - угол второй четверти, тогда ∠CBD = arccos(-1/7)
∠CAD = arccos(-1/7)
ответ: arccos(-1/7).
ответ:ответ на фото,удачи:)
Объяснение: