Объяснение:
В параллелограмме противолежащие стороны равны и противолежащие углы равны.
Доказательство:
Противолежащие стороны параллелограмма параллельны.
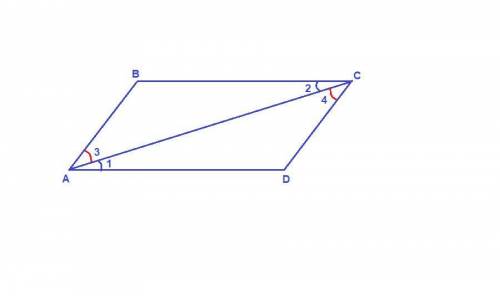
∠1 = ∠2 как накрест лежащие при пересечении параллельных прямых ВС и AD секущей АС,
∠3 = ∠4 как накрест лежащие при пересечении параллельных прямых АВ и СD секущей АС,
АС - общая сторона для треугольников АВС и CDA,
значит ΔАВС = ΔCDA по стороне и двум прилежащим к ней углам.
Тогда ∠В = ∠D, AB = CD и BC = AD.
∠BAD = ∠1 + ∠3
∠BCD = ∠2 + ∠4,
∠1 = ∠2 и ∠3 = ∠4, ⇒ ∠BAD = ∠BCD
Пусть Н - середина стороны ВС.
АН⊥ВС как медиана и высота правильного треугольника АВС,
SH⊥ВС как медиана и высота равнобедренного треугольника SBC.
∠SHA = 45° - линейный угол двугранного угла между плоскостью боковой грани и плоскостью основания.
ΔSOH: ∠SOH = 90°, ∠SHO = 45°, значит это равнобедренный прямоугольный треугольник, тогда
ОН = SH = 4 м, SH = 4√2 м
ОН - радиус окружности, вписанной в правильный треугольник:
ОН = АВ√3/2
АВ = 2 · ОН / √3 = 2 · 4 / √3 = 8√3/3 м
Sбок = 1/2 Pосн · SH
Sбок = 1/2 · 3 · 8√3/3 · 4√2 = 16√6 м²