В трапеции ABCD биссектриса угла BAD проходит через точку М, которая является серединой CD. Известно, что АВ=5, АМ=4. Найдите длину отрезка ВМ.
По условию СМ=CD.
Решить задачу можно разными
Проведем МК || AD - по т. Фалеса она делит АВ в отношении DM:MC т.е. на АК=КВ.
В ∆ АКМ ∠КМА= ∠МАD - как накрестлежащие.
∠МАD=∠МАК- как половины ∠КАD
∠КАМ=∠КМА⇒
∆ АКМ - равнобедренный, и АК=КМ.
Но КМ=АК=КВ ⇒ ∆ ВКМ равнобедренный, ⇒ ∠КВМ=∠КМВ.
Углу КМВ равен накрестлежащий ∠ СВМ. ⇒ ВМ - биссектриса угла СВК.
В трапеции сумма углов, прилежащих к одной боковой стороне, равна 180º
Тогда сумма их половин равна 90º, и угол ВМА=180º-90º=90º
∆ АВМ - прямоугольный. Отношение катета АМ к гипотенузе АВ 3:5⇒ ∆ АВМ - египетский, и ВМ=3 (ед. длины) ( по т.Пифагора получим ту же величину).
Доказав, что ∆ АКМ - равнобедренный, проведем в нем высоту КН. Она же - медиана, и АН=НМ.
Тогда КН - средняя линия ∆ АВМ, и КН || ВМ, откуда следует, что угол ВМА=90º, ∆ АВМ - египетский и ВМ=3 (ед. длины).
на любителей т. косинусов)
По т. косинусов можно из ∆ КАМ найти косинус угла КАМ, затем по ней той же теореме длину ВМ.
Вычисления приводить не буду - пользовалась при нахождении косинуса инженерным калькулятором. Без него значения будут лишь приближенными. Таким образом найден
cos ∠КАМ=0,8.
Тогда ВМ²=5²+4²-2•5•4•0,8 ⇒
BM²=25+16-32=9
BM=3 (ед. длины)

Пошаговое решение:
Дано: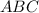 ;
;
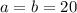 см;
см;
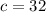 см;
см;
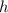 - высота;
- высота;
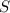 △
△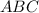 ;
;
 равнобедренного треугольника представляет из себя гипотенузу. За катет берём получившуюся в результате раздела основания на две равные части сторону. По теореме Пифагора находим оставшийся катет, что и будет выступать в роли высоты.
равнобедренного треугольника представляет из себя гипотенузу. За катет берём получившуюся в результате раздела основания на две равные части сторону. По теореме Пифагора находим оставшийся катет, что и будет выступать в роли высоты.
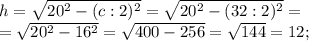
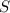 △
△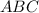
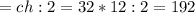 (см²)
(см²)
△
Найти:
Решение:
Высота в равнобедренном треугольнике является одновременно и медианой, и биссектрисой. Медиана, проведённая из вершины угла в противоположную сторону, делит её на две равные части. Соответственно, проведённая из противоположного основанию угла высота делит его пополам. Перпендикуляр образует два прямоугольных треугольника. Боковая сторона
Находим площадь, умножив основание на высоту и поделив на 2.