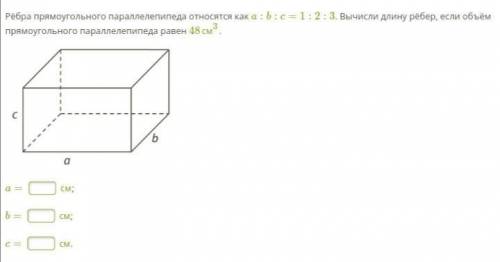
Дано: RSQT-трапеция , ∠SRK=∠QTK=45°,RE=ES=TF=FQ, SQ=10 ,SK=8, SK⊥RT. Найти: RT,EF.
Объяснение:
Т.к. RE=ES=TF=FQ ⇒ RS=TQ ⇒ RSQT- равнобедренная трапеция.
Для равнобедренной трапеции справедливо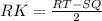 
(*).
Из прямоугольного ΔRKS найдем RK : тк один из острых углов 45°, то и другой острый угол 45°⇒ ΔRKS- прямоугольный равнобедренный ⇒SK=RK=8. Получаем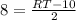 
или RT=26 .
EF-средняя линия , т.к. по условию она проходит через середины сторон RS ,TQ ⇒ EF=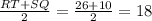 
=================================
(*) Высота , опущенная из вершины на большее основание , делит его на большой отрезок , который равен полусумме оснований и меньший- равен полуразности оснований.
Сторони трикутника 6;10;14
Объяснение:
За властивістю середної лінії сторона трикутника проти якої лежить середня лінія у два рази більша ніж середня лінія, тоді сторони трикутника відносяться як 6 : 10 : 14.Введемо коефіціент пропорційності x і складемо рівняння, так як сума усіх сторін дорівнює периметру трикутника.Нехай сторони трикутника a,b,c і нехай a = 6x, b = 10x, c = 14x.
P трикутника = a + b + c
30 = 6x + 10x + 14x
30 = 30x; x = 1
Отже сторони трикутника a = 6 * 1 = 6, b = 10 * 1 = 10, c = 14 * 1 = 14
Пусть х - составит часть тогда из отношения a:b:c=1:2:3
а=х, b=2x, c=3x
Формула объема параллелепипеда V=abc=48 см³
⇒ x × 2x × 3x=48
6x³=48
x³=8
x=∛8=2 см одна часть
a=2 см b=4 см c=6 см