
≈6π ед.
Объяснение:
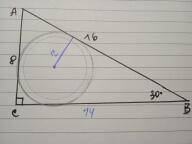
Дано: ΔАВС - прямоугольный, ∠С=90°, ∠В=30°, АВ=16
длина вписанной окружности - ?
АС=1/2 АВ = 16:2=8 ед. по свойству катета, лежащего против угла 30°
По теореме Пифагора
ВС=√(АВ²-АС²)=√(256-64)=√192≈14 ед.
r=(АС+ВС-АВ):2=(8+14-16):2≈3 ед.
с=2πr=2π*3≈6π ед.
* * * * * * * * * * * * * * * * * * * * * * * * * *
В равнобедренной трапеции диагональ является биссектрисой. Найдите площадь трапеции, если боковая сторона - 25 см, основание 39 см
ответ: 768 см².
Объяснение: Пусть ABCD равнобедренная трапеция
AD и BC основания трапеции ( AD || BC ) AD =39 см ,
ВA = CD =25 см и ∠ BAC = ∠ DAC .
S(ABCD) = h*(AD+BC)/2 -?
--------------------------------------
∠ BCA= ∠ DAC как накрест лежащие углы ( BC || AD , CA секущая) ,
следовательно ∠ BCA= ∠ DAC =∠ BAC , т.е. ΔBAC равнобедренный
BA = BC =25 см получили BA = CD =25 см .
Проведем BB₁ ⊥ AD и CC₁ ⊥ AD . BCC₁B₁ _прямоугольник BB₁ =CC₁
B₁C₁ = BC =25 см ; Δ BB₁A = Δ CC₁D(гипотен. BA= CD и катеты BB₁ =CC₁).
AB₁ =(AD - BC)/2 =(39 - 25)/2 см=7 см .
Из Δ BB₁A по теореме Пифагора:
BB₁ =√(BA² -AB₁² ) =√(25² -7)² =√(625 -49) =√576=24 (см) .
* * * h=√(25²-7)² =√(25 -7)(25 +7) =√(18*32) √(9*2*16*2)=3*2*4=24 * * *
S(ABCD) = h*(AD+BC)/2 =24(39+25)/2 =24*32 = 768 (см²).

66 см²
Объяснение:
Медианы треугольника пересекаются в одной точке, и точкой пересечения делятся в отношении 2:1, считая от вершины.
⇒ ВМ:МК=2:1.
У ΔАМК и ΔАВМ одна и та же высота АН - перпендикуляр, проведенный из вершины А к прямой ВК, содержащей стороны ВМ и МК этих треугольников.
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты) ⇒
Samk/Sabm=1/2 ⇒
11/Sabm=1/2 =>
22=Sabm.
Sabk=22см²+11см²=33см²
медиана ВК делит ΔАВС на два равновеликих т.е Sabk = Skbc.
⇒
Sabc=33*2=66см²
AB=16
∠B=30°
По теореме синусов, стороны пропорциональны синусам противолежащего угла.
(Ну короче на будущее, катет прямоугольного треугольника лежащий напротив угла 30° равен половине гипотенузы)
Радиус вписанной окружности в прямоугольный треугольник вычисляется по формуле:
a и b – катеты, c – гипотенуза
a=8
c=16
Найдем b по теореме Пифагора
(Еще раз на будущее катет прямоугольного треугольника, лежащий напротив угла 60°, в √3 раза больше, чем катет который напротив 30°)
Теперь найдём радиус:
Длина окружности:
L=2πr
Можно дальше скобки раскрыть, если понадобится.
Но я думаю это необязательно