Найдите расстояние от точки А(0;4;3) а) до начала координат ; б) до оси аппликат; в) до координатной плоскости хOу.

👇

Ответ:

senazubik63kfkd

07.02.2023

Дано: А (-3; 4; -4), Следовательно, точка А1 — проекция точки А на Оху — имеет координаты A1 (-3; 4; 0),

A2 — проекция точки А на Оуz — имеет координаты: A2 (0; 4; -4), A3 — проекция точки А на Oxz — имеет координаты: A3 (-3; 0; -4). По формуле

расстояния между двумя точками

Найдем

таким образом для А (х; у; z) расстояниями до координатных плоскостей будут |x|, |y| и |z|.

б) На ось Ox проекция A1 точки А имеет координаты А1 (-3; 0; 0), на Oy: A2 (0; 4; 0), на Oz: A3 (0; 0; -4).

4,4(8 оценок)

Открыть все ответы

Ответ:

1zoya

07.02.2023

Четырехугольник может быть описан около окружности тогда и только тогда, когда суммы длин его противоположных сторон равны.

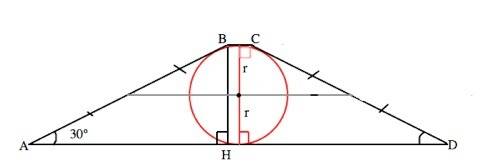
Трапеция - четырехугольник. Сумма оснований описанной трапеции равна сумме боковых сторон и вдвое больше средней линии.

АВ+СD=2•8,5=17 см Трапеция равнобедренная, поэтому АВ=СD=8,5

Угол ВАD=∠СDA= 30°, ⇒ высота ВН трапеции равна половине АВ.

ВН=8,5:2=4,25 см

Диаметр окружности, вписанной в трапецию, перпендикулярен её основаниям и равен её высоте.

R=D:2=4,25:2=2,125 см.

20 ! длина средней линии равнобедренной трапеции abcd ,описанной около окружности равен 8,5 см,а ост

4,5(15 оценок)

Ответ:

pudovkinao

07.02.2023

Если воспользоваться готовой формулой для радиуса вписанной в правильный тетраэдр сферы - то всё попроще. но попробуем обойтись без этой формулы.
на первом рисунке изображён тетраэдр и сечение вписанной сферы плоскостью СРТ
Низ красный, верх синий
Примем сторону тетраэдра за 1. тогда в треугольнике АКР
АР = 1/2
∠РАК = 30°
КР/АР = tg(30) = 1/√3
КР = 1/(2√3)
КР/АК = sin(30°)
АК = 2*КР = 1/√3
И так как К - точка пересечения медиан основания, то
СК = АК = 1/√3
Переходим к ΔАРТ
РТ²+АР² = АТ²
РТ² + 1/4 = 1
РТ² = 3/4
РТ = √3/2
Переходим к ΔКРТ
КТ²+1/(2√3)² = (√3/2)²
КТ²+1/(4*3) = 3/4
КТ² = 3/4-1/12 = 9/12-1/12 = 8/12 = 2/3
КТ = √(2/3) - это высота пирамиды
Пора искать радиус вписанной сферы
ΔКРТ и ΔХОТ подобны - общий угол Т, по прямому углу и третий угол равен в силу того, что два равны и сумма углов треугольника 180°
ОХ = ОК = r
КР/ОХ = РТ/ОТ
1/(2√3)/r = √3/2/(√(2/3)-r)
(√(2/3)-r)/(2√3) = √3/2*r
√(2/3)-r = 2√3√3/2*r
√(2/3)-r = 3r
√(2/3) = 4r
r = 1/(2√2√3) = 1/(2√6)
Хорошо :)
В правильный тетраэдр с единичным ребром можно вписать сферу радиуса 1/(2√6)
Если радиус сферы R, то ребро тетраэдра будет a = 1/(1/(2√6)) = 2√6
площадь одной грани
S₁ = 1/2*a²*sin(60°) = 2*6*√3/2 = 6√3
И полна плошадь тетраэдра в 4 раза больше
S = 24√3

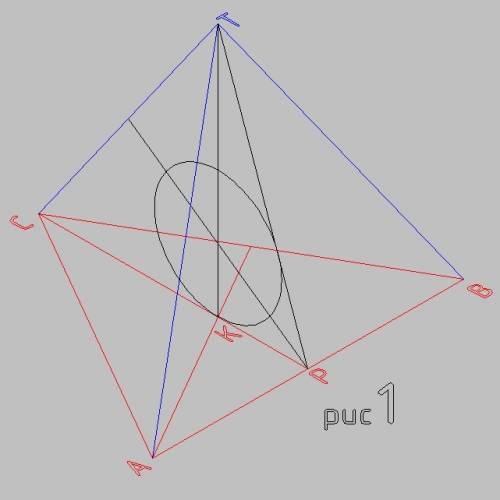
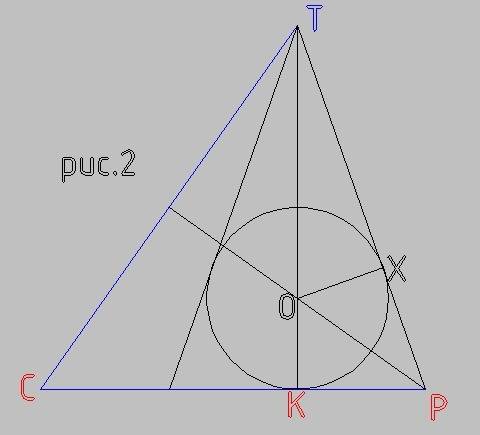
Около шара радиуса r описан правильный тетраэдр. найдите площадь поверхности тетраэдра. с рисунком,