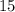см.
Проведём отрезк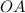и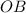 
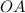и 
.
=======================================================
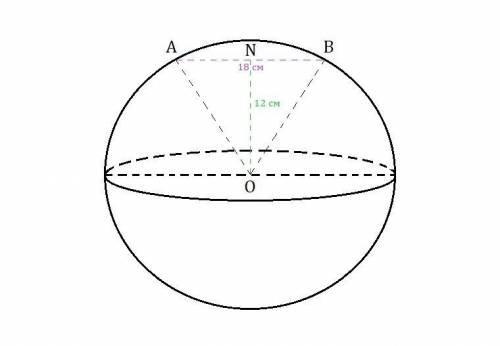
и 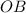- радиусы данной сферы ⇒ они равны.
⇒ 
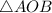- равнобедренный, где 
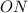- расстояние от точки 
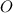до прямой 
и высота равнобедренного
Высота, проведённая из вершины равнобедренного треугольника к основанию равнобедренного треугольника, является биссектрисой и медианой.
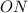⇒ - высота, медиана и биссектриса.
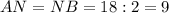см, так как 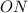- медиана.
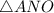- прямоугольный, так как 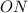- высота.
Найдём радиус 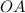по теореме Пифагора 
.
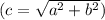см.
Итак, радиус данной сферы = 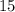см.
2) Радиусом А1D совершаем поворот на 45°против часовой стрелки (в положительном направлении) Получаем точку А.
3) Радиусом В1D совершаем поворот на 45° против часовой стрелки.
Замеряем циркулем А1В1 и откладываем этот отрезок от точки А до пересечения с первой дугой. Получили вершину В.
4) Замерим циркулем С1D и проводим дугу радиусом С1D
Циркулем замеряем сторону В1С1 и от точки В проводим дугу до пересечением с предыдущей дугой, получили точку С.
5) соединяем точки АВСD получили искомый прямоугольник. см фото