В объяснении.
Объяснение:
1. Сумма внутренних углов выпуклого четырехугольника равна 360 градусов.
Пусть коэффициент пропорциональности равен х.
Тогда х+2х+3х+4х = 360° => х = 36°.
Больший угол равен 4х = 144°.
2. Сумма внутренних углов выпуклого четырехугольника равна 360 градусов.
Пусть коэффициент пропорциональности равен х.
Тогда х+2х+2х+4х = 360° => х = 40°.
Меньший угол равен 4х = 40°.
3. Площадь квадрата равна площади прямоугольника: 4*9 = 36 =>
Сторона квадрата равна √36 = 6 ед.
4. Площадь прямоугольника равна х*(х+2) = 24. Тогда
х² + 2х - 24 = 0. Решаем квадратное уравнение. => x = 6. (второй корень отрицательный)
Тогда большая сторона равна 6 + 2 = 8 ед.
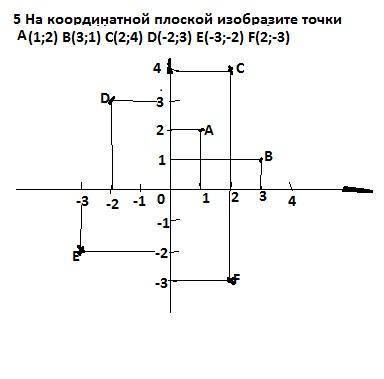
5. Смотри рисунок.
6. Уравнение окружности:
(Х - Хц)² + (Y-Yц)² = R² Тогда
а) Координаты центра: Ц(-5;2) Радиус = 4 ед.
б) Координаты центра: Ц(0;-3) Радиус = 3 ед.
Тк ABCD - ромб, то все стороны = 10 см. угол А =С=60 градусам, угол В=D=120 градусам. BD - диагональ = 10 см. В ромбе диагонали перпендикулярны, точкой пересечения делятся пополам, являются биссектрисами углов; следовательно угол DBC = 60 градусам. О - точка пересечения диагоналей, ВО=ОD=5 см. Треуг. BOC - прямоугольный, значит СО можно найти по т. Пифагора. Диагональ СA = 2СО. Потом просто находишь по формуле площадь ромба ( площадь ромба равна полусумме произведения его диагоналей)
В расчетах могла ошибиться, но ход решения должен быть верный.