Длина гипотенузы равна сумме длин этих отрезков: 18см + 32 см = 50 см. Высота в прямоугольном треугольнике является средним геометрическим для проекций на гипотенузу, т.е. высота равна √32•18 = √576 = 24 см. Катетов можно найти по теореме Пифагора: √24² + 18² = √576 + 324 = √900 = 30 см. √50² - 30² = √2500 - 900 = √1600 = 40 см. ответ: 30.
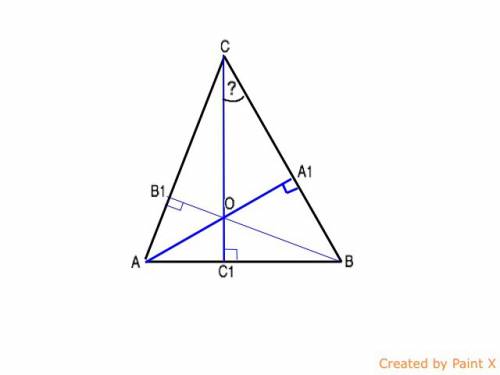
Высоты перпендикулярны стороне, к которой проведены.
В прямоугольном треугольнике АА1В катет ВА1 равен половине гипотенузы АВ.
Т.е. А1В:АВ=0,5 - это синус угла 30°⇒
∠А1АВ=30°⇒
∠АВА1=60°
Высоты треугольника пересекаются в одной точке (теорема).
Продолжим СО до пересечения с АВ в точке С1.
Через две точки (С и О )можно провести прямую, и только одну. (аксиома)⇒
СС1 - высота и ∆ СС1В - прямоугольный, в котором острый угол СВС1=60°
Сумма острых углов прямоугольного треугольника равна 90°⇒
∠ ОСВ= 90°-60°=30°
>
Объяснение: