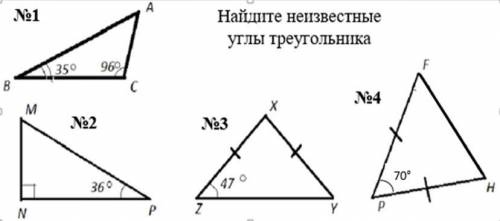
1) A + B + C = 180° (по теореме о сумме углов в треугольнике)
А = 180° - (B + C)
A = 180° - (35 + 96)
A = 180° - 131
A = 49°
ответ: А = 49°
2) M + N + P = 180° (по теореме о сумме углов в треугольнике)
M= 180° - (N + P)
M = 180° - (90+ 36)
M = 180° - 126
M = 54
ответ: А = 54°
3) ZX = XY => треугольник ZXY - р/б => Z = Y = 47°
Z + X + Y = 180° (по теореме о сумме углов в треугольнике)
X = 180° - ( Z + Y)
X = 180° - (47 + 47)
X = 180 - 94
X = 86
ответ: X = 86°
4) PF = PH => треугольник PFH - р/б => F = H
P + F + H = 180° (по теореме о сумме углов в треугольнике)
F + H = 180° - P = 180° - 70° = 110°
F = H = 110:2 = 60°
ответ: F = H = 60°
Находим основания медиан (точки пересечения медиан со сторонами).
А₁(Ха1;Уа1) Хв+Хс Ув+Ус х у
2 2 А₁ 4 0
В₁(Хв1;Ув1) Ха+Хс Уа+Ус х у
2 2 В₁ -2 -2
C₁(Хс1;Ус1) Ха+Хв Уа+Ув х у
2 2 С₁ 0 4.
Длины медиан:
АА₁ = √((Ха1-Ха)²+(Уа1-Уа)²)) = √104 ≈ 10,19803903
BB₁ = √((Хв1-Хв)²+(Ув1-Ув)²)) = √128 ≈ 11,3137085
CC₁ = √((Хc1-Хc)²+(Уc1-Уc)²)) = √104 ≈ 10,19803903
ответ: сумма длин медиан равна 31,70978655.
1) 180-(35+96)=49 2) 180-(36+90)=54 3) 180-(47+47)= 86 4) (180-70):2= 55