104 см
Объяснение:
Дано
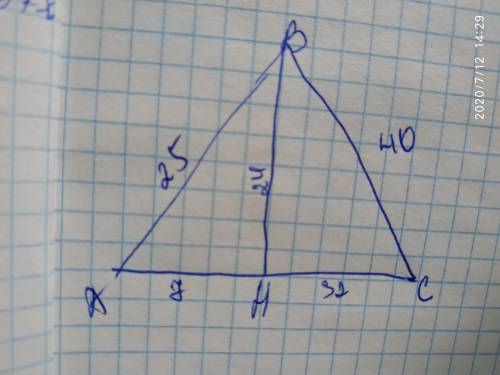
Трикутник ∆АВС
АВ=25 см
ВС=40 см
АН=7
ВН=? висота
АС=? сторона трикутника
Р∆АВС=? периметр трикутника
Рішення.
∆АВН прямокутний, ВН і АН - катети.
АВ- гіпотенуза.
За теоремою Піфагора знайдемо ВН
ВН²=АВ²-АН²=25²-7²=625-49=576 см
ВН=√576=24 см.
∆ВНС- прямокутний, ВН і НС - катети, ВС- гіпотенуза.
За теоремою Піфагора знайдемо НС
НС²=ВС²-ВН²=40²-24²=1600-576=1024 см
НС=√1024=32 см
АС=АН+НС=7+32=39 см
Р∆АВС=АВ+ВС+АС=25+40+39=104 см периметр трикутника.
Відповідь: периметр трикутника дорівнює 104 см
Пусть О — точка пересечения высоты BD и биссектрисы AE.
AO : OE = 23 : 13, BD = 12 см. По теореме Менелая для треугольника АЕС имеем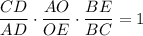
. Поскольку треугольник ABC равнобедренный, то BD является биссектрисой и медианой, т.е. AD = DC, тогда 
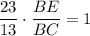(1).
По свойству биссектрисы: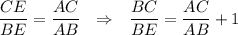
.
По теореме Пифагора из прямоугольного треугольника BDC:
Подставляем в равенство (1), получим уравнение относительно АС.
Решаете как иррациональное уравнение, возводите два раза обе части уравнения и вы должны придти к биквадратному уравнению , получите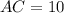
см.
Площадь треугольника: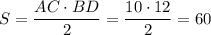
см²
ответ: 60 см².