Δ АВС - равнобедренныйВК = 30 см - биссектриса к основанию АС, она же и медиана Δ АВС ⇒ АК=КСNM = 16 см - средняя линия II АС ⇒AN=NBNK = ? - средняя линия II ВС NM x ВК в т.О и деляться ей пополам, т.к. Δ NMB подобен Δ АВС по 3-м углам, ⇒ Δ NMB равнобедренный и ВО его высота, биссектриса и медиана. ВО=ВК т.к. NM средняя линия Δ АВСПолучаемNO=1/2NM= 16/2=8OK=1/2ВК= 30/2=15Δ NOK прямоугольный, т.к. уже доказано, что BO высота Δ NMB ⇒ <BON = 90°<NOK - смежный и =180°-<BON = 90°По теореме Пифагора находим NK - гипотенузу Δ NOK NK=√(NO²+OK²) = √(8²+15²)=√(64+225)=√289=17 см
1. ΔАВС: ∠АВС = 90°, ∠ВАС = 30°, tg30° = BC / AB 1/√3 = 6 / AB AB = 6√3 см
2. Sabcd = ab = 192 Pabcd = 2(a + b) = 56
Получаем систему уравнений: ab = 192 a + b = 28
b = 28 - a 28a - a² = 192 решим второе
a² - 28a + 192 = 0 D/4 = 14² - 192 = 196 - 192 = 4 a = 14 + 2 = 16 или a = 14 - 2 = 12 b = 12 b = 16
Итак, стороны прямоугольника 12 см и 16 см. МО - перпендикуляр к плоскости прямоугольника. Наклонные, проведенные из точки М, равны, значит равны и их проекции, т.е. АО = ОВ = ОС = OD, ⇒ О - точка пересечения диагоналей. ΔАВС: ∠АВС = 90°, по теореме Пифагора АС = √(АВ² + ВС²) = √(256 + 144) = √400 = 20 см ОА = 10 см
Составьте уравнение плоскости, перпендикулярной вектору АВ и проходящей через точку В, если А(-2;1;3), В(1;-2;4).
Объяснение:
Координаты вектора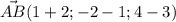
или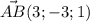 
.
Уравнение плоскости, проходящей через точку М( х₀;у₀;z₀) и перпендикулярно вектору m(α;β;γ) имеет вид α(х-х₀)+β(у-у₀)+γ(z-z₀)=0
Тогда равнение плоскости, проходящей через точку В(1;-2;4) и перпендикулярно вектору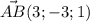
имеет вид
3(х-1)-3(у+3)+1(z-1)=0,
3x-3y+z-13=0