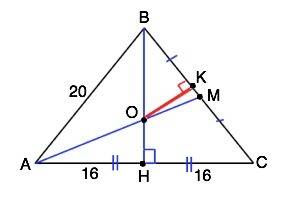
Обозначим медианы ВН и АМ.
В равнобедренном треугольнике медиана, проведенная к основанию, является высотой и биссектрисой. =>
∆ АВН - прямоугольный, АН=СН=32:2=16 см
По т.Пифагора
ВН=√(AB²-AH²)=√(400-256)=12
Медианы треугольника точкой пересечения делятся в отношении 2 :1, считая от вершины.=>
ВО=ВН•2/3=8
ОН=ВН:3=4
Из прямоугольного ∆ АОН по т.Пифагора
АО=√(AH*+OH*)=√(256+16)=√272=4√17
Расстояние от точки до прямой измеряется длиной отрезка, проведенного от точки перпендикулярно к прямой.
ОК⊥ВС
Прямоугольные ∆ ОКВ и ∆ ВНС имеют общий острый угол при В. => они подобны.
ОВ:ВС=ОК:НС
8:20=ОК:16 =>
20•ОК=128
ОК=6,4 (см)
Відповідь:
Пояснення:
Нехай точки M , N , K - cередини сторін АС , АВ , ВС тр - ника
АВС відповідно . 1) Сполучимо точки M , N , K ; сторони
утвореного тр - ника MNK є середніми лініями шуканого ΔАВС .
2) Проведемо пряму m║NK через т. М .
3) Проведемо пряму n║MK через т. N ; m ∩ n = A .
4) Проведемо пряму k║MN через т. K ; m ∩ k = C ; n ∩ k = B .
ΔABC є шуканим тр - ником .
2) Сполучаємо послідовно дані точки М , N , K , P . Як відомо
утвориться паралелограм , сторони якого є середніми лініями
шуканого 4 -кутника . Далі по аналогії із попередньою задачею
проведемо по - порядку чотири прямі ,паралельні сторонам
АВСD і так далі .