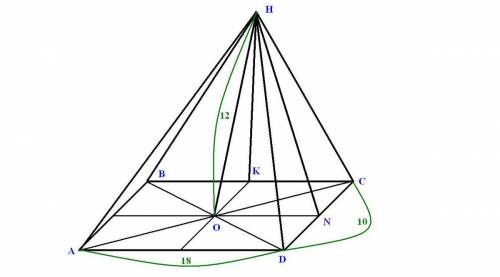
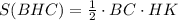 , где НК - высота, проведенная к стороне ВС. НК можно найти как гипотенузу прямоугольного треугольника НОК, где ОК - половина стороны СD.
, где НК - высота, проведенная к стороне ВС. НК можно найти как гипотенузу прямоугольного треугольника НОК, где ОК - половина стороны СD.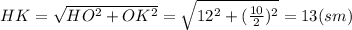 .
.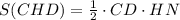 , где НN - высота, проведенная к стороне СD.
, где НN - высота, проведенная к стороне СD.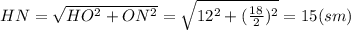
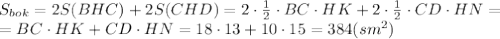
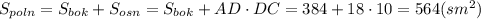
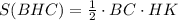 , где НК - высота, проведенная к стороне ВС. НК можно найти как гипотенузу прямоугольного треугольника НОК, где ОК - половина стороны СD.
, где НК - высота, проведенная к стороне ВС. НК можно найти как гипотенузу прямоугольного треугольника НОК, где ОК - половина стороны СD.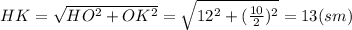 .
.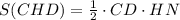 , где НN - высота, проведенная к стороне СD.
, где НN - высота, проведенная к стороне СD.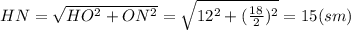
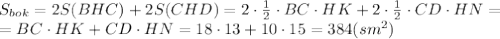
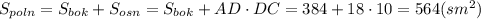

ответ: CE=9 см, ЕА=15 см.
Объяснение:
По теореме Пифагора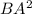 =
= 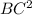 +
+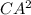 ⇒
⇒
CA= =
=  =
=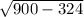 =
=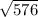 =24см
=24см
Пусть СЕ=х, тогда ЕА=24-х
По свойству биссектрисы в треугольнике:
Имеем:
30x=18(24-x)
30x=432-18x
30x+18x=432
48x=432
x=432:48
x=9
Тогда CE=x=9 см, ЕА=24-х =24-9=15 см.
ответ: CE=9 см, ЕА=15 см.