1)Треугольник AOB равен тр-ку COD по 2 сторонам и углу между ними. Т.к они равны, то соотв. элем. равны. Угол OCD равен углу OBA - они накрест лежащие при прямых АВ и CD и сек. ВС. Следовательно, AB ║CD
2)Треугольники OXY и OZY равны по 3 сторонам. Т.к они равны, то соотв. элем. равны. Угол XOY равен углу YZO - они накрест лежащие при прямых OX и YZ и сек. OY. Следовательно, OX ║YZ. Также угол XYO = углу YOZ(из равенства тр-к) - они накрест лежащие при прямых OX и YZ и сек. OY. Следовательно, OZ ║XY
3)Треугольники ROB и SOT равны по стороне и двум прилежащим к ней углам. Т.к они равны, то соотв. элем. равны. Угол BRO = углу STO - они накрест лежащие при прямых RB и ST и сек. BS. Следовательно, RB ║ST. Также треугольники ROS и BOT равны по стороне и 2 прилежащим к ней углам. Отсюда угол SRO = углу BTO - они накрест лежащие при прямых RS и BT и сек. RT. Следовательно, RS ║BT.
Так как отрезки РР₁ и ММ₁ перпендикулярны плоскости а, то указанные отрезки лежат на одной плоскости, а точка Р₁ лежит на отрезке КМ₁.
Рассмотрим ∆КРР₁ и ∆КММ₁.
Угол МКМ₁ – общий;
Угол КР₁Р=угол КМ₁М (оба прямые, так как РР₁ и ММ₁ перпендикулярны КМ₁)
Следовательно ∆КРР₁~∆КММ₁ по двум углам.
Пусть КР=n, тогда РМ=2n (из отношения КР:РМ=1:2), следовательно КМ=KP+PM=n+2n=3n.
Отношение двух любых сторон одного треугольника, равно отношению двух соответствующих сторон треугольника, подобного первому. Тогда:
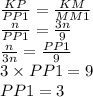
ответ: 3 см
Построим △DCB, равный △ABC.
DB=AC=BM
∠DBM=80-20=60
△DBM - равносторонний (р/б с углом 60)
△DMC=△BMC (по трем сторонам)
∠DCM=∠BCM=20/2=10
∠MCA=80-10=70°