Печально, что ты такая(
Кста спс за красивый почерк
Это равно бедренный треугольник, т.к только в нем высота является медиаоной и биссектрисой следовательно
Угол С делиться пополам и мы получаем 2 угла по 45 градусов.
Рассмотрим треугольник CDA, угол D=90 градусов по условию, угол ACD(сори за ляп, я ***) равен 45 градусов, следовательно Угол А равен тоже 45 градусов, так как сумма углов в треугольнике составляет 180 градусов, следовательно треугольник CDA ТОЖЕ РАВНОБЕДРЕННЫЙ и это означает, чо CD=DA=5см
ответ: 5 см.
Я хоть и 9 класс и такие классы решаю как орешки, но это сложно было..
Кста оформи под стиль, который училька просит.
Объяснение:
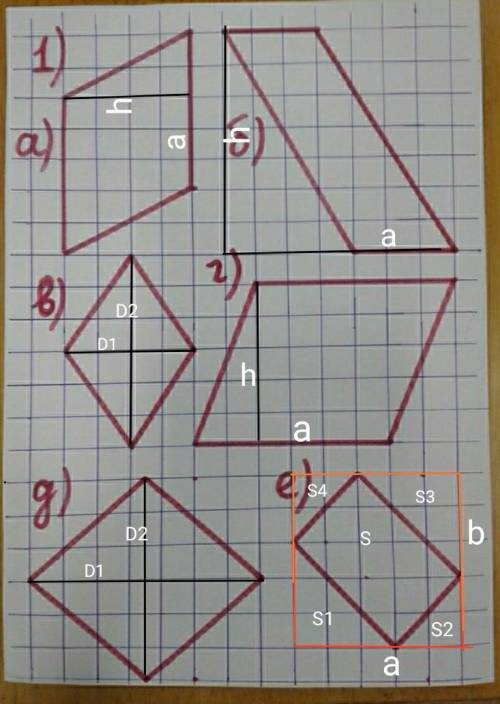
а)
Фигура параллелограм.
a=5 кл
h=4кл
S=?
Решение.
S=a*h
S=5*4=20
ответ: 20 кл²
б)
Фигура параллелограм.
а=3кл
h=7кл
S=?
Решение
S=a*h
S=3*7=21 кл²
ответ: 21кл²
в) фигура ромб.
D1=4кл
D2=6кл
S=?
Решение
S=1/2*D1*D2
S=6*4/2=12 кл²
ответ: 12кл²
г) фигура параллелограм
а=6кл
h=5кл
S=?
Решение
S=a*h
S=5*6=30кл²
ответ: 30кл²
д) Фигура ромб
D1=7кл
D2=6кл
S=?
Решение
S=1/2*D1*D2
S=7*6/2=21кл²
ответ: 21кл.
е)
Фигура прямоугольник
S=a*b-2*S1-2*S2
S1=S3
S2=S4
Площадь прямоугольного треугольника равна половине произведения двух катетов.
S1=1/2*3*3
S2=1/2*2*2
S=5*5-2*3*3*1/2-2*2*2*1/2=25-9-4=12кл²
ответ: 12кл²
ΔАВС - равнобедренный , АВ=ВС , BD ⊥AC ,
ВО ⊥ плоскости α ⇒ ВО перпендикулярна любой прямой в плоскости α . Проведём прямую DО , тогда DО ⊥ BO и ΔВOD - прямоугольный , ∠BOD=90° . Тогда BD - наклонная , а DO - проекция наклонной BD на плоскость α .
BD ⊥ AC , так как BD - высота равнобедренного треугольника АВС .
По теореме о трёх перпендикулярах : если прямая, проведенная на плоскости через основание наклонной, перпендикулярна самой наклонной, то она перпендикулярна и её проекции .
Точка D - основание BD . Наклонная BD перпендикулярна прямой АС, тогда и её проекция DO перпендикулярна прямой AC.
Получили, что АС ⊥ BD и АС ⊥ DO . По признаку перпендикулярности прямой и плоскости, прямая АС будет перпендикулярна плоскости, в которой лежат прямые BD и DO , то есть плоскости BDO . Что и требовалось доказать .