Question

Кут при основі рівнобедреного трикутника дорівнює 30градусів. Радіус кола, описаного навколо трикутника, дорівнює 4 см. Визначити радіус кола, вписаного в даний трикутник.

Answer 1

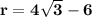ответ:   $\bf r=4\sqrt3-6$   см  .

ΔАВС - равнобедренный , АВ=ВС .  ∠А=∠С=30°  .  R - радиус описанной окружности , r - радиус вписанной окружности ,  R=4 cм .  Найти:  r .

      По теореме синусов имеем  

$\dfrac{BC}{sinA}=2R\ \ \Rightarrow \ \ \ BC=2R\, sinA=2\cdot 4\cdot sin30^\circ =8\cdot \dfrac{1}{2}=4$  см .

   Опустим перпендикуляр ВН из вершины В на основание АС . Точка Н будет серединой основания АС .

    Найдём  АН  из ΔABH .

 $cosA=\dfrac{AH}{AB}\ \ \ \Rightarrow \ \ \ AH=AB\cdot cosA=4\cdot cos30^\circ =4\cdot \dfrac{\sqrt3}{2}=2\sqrt3$  см  

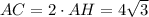     Тогда   $AC=2\cdot AH=4\sqrt3$  м .

  Известна формула площади треугольника через радиус вписанной окружности :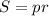  $S=pr$  ,  где  р - полупериметр .  Отсюда можно выразить радиус вписан. окр-ти    $r=\dfrac{S}{p}$  .

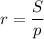    Найдём полупериметр ΔABС .

$p=\dfrac{1}{2}\cdot (AB+BC+AC)=\dfrac{1}{2}\cdot (4+4+4\sqrt3)=2\cdot (2+\sqrt3)=4+2\sqrt3$   см .

Теперь найдём площадь треугольника АВС .

$S=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinA=\dfrac{1}{2}\cdot 4\cdot 4\sqrt3\cdot sin30^\circ =8\sqrt3\cdot \dfrac{1}{2}=4\sqrt3$   см²  

$r=\dfrac{S}{p}=\dfrac{4\sqrt3}{2\cdot (2+\sqrt3)}=\dfrac{2\sqrt3\, (2-\sqrt3)}{(2+\sqrt3)(2-\sqrt3)}=\dfrac{2\sqrt3\, (2-\sqrt3)}{4-3}=4\sqrt3-6$  см