Question

Хелп

В треугольник ABC вписана окружность, касающаяся стороны BC, в точке D. Известно, что AD=DC, косинус угла BCA равен 2/3 и сторона BC = 9. Найдите радиус вписанной окружности.

Answer 1

ответ.

  ΔАВС , точки  Д , К М - точки касания вписанной окружности сторон треугольника , АД=ДС , cosC=2/3 , ВC=9 . Найти r .

  Так как АД=ДС , то ΔАДС - равнобедренный . Проведём в нём высоту ДН .  Тогда АН=НС . Обозначим АН=НС=х , тогда АС=2х .

И найдём ДС .

ДС=х/cosC=3x/2

Так как отрезки касательных, проведённых из одной точки к окружности равны, то КС=ДС=3х/2 .

Аналогично, ВД=ВМ и АК=АМ .

ВД=ВС-ДС=9-3х/2  ,   АК=АС-КС=2х-3х/2=х/2

АВ=АМ+ВМ=х/2+(9-3х/2)=9-х

Применим теорему косинусов к ΔАВС .

$AB^2=AC^2+BC^2-2\cdot AC\cdot BC\cdot cosC(9-x)^2=4x^2+81-2\cdot 2x\cdot 9\cdot \dfrac{2}{3}81-18x+x^2=4x^2+81-24x3x^2-6x=0\ \ ,\ \ 3x(x-2)=0\ \ ,\ \ x_1=0\ ,\ x_2=2$  

Значение 0 не подходит по смыслу . Значит, х=2 .

Стороны треугольника равны  $AC=2x=4\ ,\ AB=9-x=9-2=7\ ,\ BC=9$  

Известна формула  площади треугольника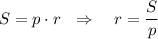  $S=p\cdot r\ \ \Rightarrow \ \ \ r=\dfrac{S}{p}$    

Полупериметр треугольника равен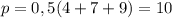  $p=0,5(4+7+9)=10$  

Площадь треугольника  по формуле Герона равна

$S=\sqrt{10(10-4)(10-7)(10-9)}=\sqrt{10\cdot 6\cdot 3\cdot 1}=6\sqrt{5}$  

Радиус вписанной окружности равен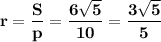  $\bf r=\dfrac{S}{p}=\dfrac{6\sqrt{5}}{10}=\bf \dfrac{3\sqrt{5}}{5}$   .