Объяснение:
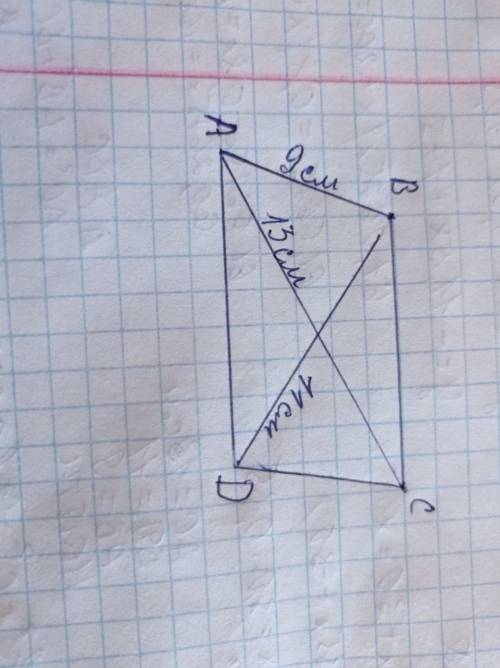
Дано:
АС = 13 см
ВD = 11 см
АВ = 9 см
Знайти: Р (АВСD) - ?
α - гострий кут між діагоналями
а² = b² + c² - 2bc *соs α
соs (180 - α) = - соs α
Розглянемо трикутник АВС по теоремі косінусів
АС² = АВ² + ВС² - 2 АВ * ВС * соs α
Розглянемо трикутник ABD
BD² = AB² + AD² - 2 AB * AD * соs α
∠A = ∠В = 180° BC = AD = x
Звідси маємо:
{13² = 9² + х² - 2* 9x* соs ∠В
{11² = 9² + х² - 2* 9x* соs ∠ А
{∠ А = 180° - ∠В => соs ∠ А = соs(180° - ∠В) = - соs ∠В
{169 = 81 + х² - 18x соs ∠В
{121² = 81 + х² + 18 x* соs ∠ B
Складемо рівняння (1) та (2)
290 = 162 + 2х²
128 = 2 х²
х² = 128 :2
х² = 64
х = 8 см
Периметр паралелограма дорівнює Р = 2 (9 + 8) = 34 (см)
Если острый угол ромба 60 градусов ,то он своей малой диагональю разбивается на два равносторонних треугольника.Тогда его малая диагональ = 4 см.Диагонали ромба перпендикулярны и делятся в точке пересечения пополам.Рассмотрим прямоугольный треугольник АОВ, уголАОВ=90,АВ=4, ОВ=2 (как половина от малой диагонали ВД).По теореме Пифагора АО=square 12 (кв.корень из 12)=2*square3. Высота ОК этого треугольника, опущенная из точки О равна (АО*ОВ)/АВ (по свойству такой высоты),значит ОК=2*2*square3/4=square3. Так как стороны ромба равноудалены от точки М, то эта точка проектируется в центр окружности, вписанной в ромб.Радиусом этой окружности будет как раз высота ОК. Из прямоугольного треугольника МОК найдем ОМ.Длина перпендикуляра ОМ и есть расстояние от точки М до плоскости ромба. По теореме Пифагора ОМ=square(MK^2-OK^2)=square(25-3)=square22.
Объяснение:
Sqrt-корень квадратный
Высота разделяет основание на 2 равные части и угол основание высоты равен 90 градусов.
Выплывает 2 треугольника: ABK и BKC, они равны.
Возьмем треугольник BKC(угол K=90,KC=3x,BC=11x).За теоремою Пифагора: 1764+9x^2=121x^2; 1764=112x^2;x^2=15,75;x=Sqrt(15,75)
r=S/p(p-полупериметр)
S=1/2*b*h=1/2*6*Sqrt(15,75)*42=126*Sqrt(15,75);
p=11*Sqrt(15,75)+11*Sqrt(15,75)+6*Sqrt(15,75)/2;
r=126*Sqrt(15,75)/11*Sqrt(15,75)+11*Sqrt(15,75)+6*Sqrt(15,75)/2
r=252*Sqrt(15,75)/11*Sqrt(15,75)+11*Sqrt(15,75)+6*Sqrt(15,75)
Сума квадратів діагоналей дорівнює сумі квадратів всіх сторін, отже:
ВД²+АС²=АВ²+ВС²+СД²+АД²
Позначимо ВС=АД=х, тоді:
13²+11²=9²+х²+9²+х²
169+121-81-81=х²+х²
128=2х²
х²=64
х=8 (см) друга сторона
Р=АВ+ВС+СД+АД=8+8+9+9=34 (см)
Відповідь: 34 см периметр паралелограма.