Question

У трикутнику АВС <С = 90°, ВС =12см, sin B =⅗ . Знайдіть периметр трикутника

Answer 1

ответ: P=36см

Объяснение:

Воспользуемся основным тригонометрическим тождеством: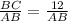
sin∠B²+cos∠B²= 1
cos∠B = прилежащий катет/гипотенуза = $\frac{BC}{AB} = \frac{12}{AB}$
Пусть AB=x

Тогда:

$(\frac{3}{5} )^{2} + (\frac{12}{x} )^{2} = 1$

$\frac{9}{25} + \frac{144}{x^{2} } = 1\\$

$\frac{9x^{2}+144*25 }{25x^{2} } = \frac{1}{1}$
$9x^{2} + 144*25 = 25x^{2}$

$16x^{2} =144*25$

$x^{2} = \frac{144*25}{16}$

$x =\sqrt{\frac{144*25}{16} }$
$x=\frac{12*5}{6}$

x=±15
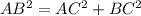
По-скольку за х мы брали сторону AB, то х может быть только положит.числом, т.е AB=15
Теперь по теореме Пифагора узнаем второй катет - AC:
$AB^{2} = AC^{2} + BC^{2}$

$AC^{2} = AB^{2} - BC^{2}$

$AC=\sqrt{15^{2} -12^{2} }$

$AC=\sqrt{225-144} =\sqrt{81} = 9$
Pabc= 9+15+12=36(см)

Answer 2

Доброї спокійної ночі.

Відповідь 36 см.

Розв'язання завдання додаю.

.