Дуга равна соответственному центральному углу.
∪CA = 360°−∪AB−∪BC = 360−96−106 = 158°
I — центр вписанной окружности в треугольник; IA = IB = IC — радиусы.
∢AIC = ∪CA = 158°; ∢AIB = ∪AB = 96°; ∢BIC = ∪BC = 106°
IA ⊥ LM, IB ⊥ MN, IC ⊥ NL (радиус ⊥ к касательной)
∢IAM = ∢MBI = ∢IBN = ∢NCI = ∢ICL = ∢LAI = 90°
∢L= 360°−∢AIC−∢LAI−∢ICL = 360−158−90−90 = 360−180−158 =180(2-1)-158=180-158 = 22° (из 4-угольника AICL)
аналогично для других углов:
∢ M= 180−96 = 84°
∢ N= 180−106 = 74°
∢L= 22°∢M = 84°∢N = 74°∪CA = 158°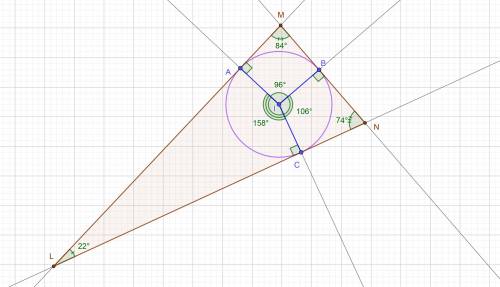
Дуга равна соответственному центральному углу.
∪CA = 360°−∪AB−∪BC = 360−96−106 = 158°
I — центр вписанной окружности в треугольник; IA = IB = IC — радиусы.
∢AIC = ∪CA = 158°; ∢AIB = ∪AB = 96°; ∢BIC = ∪BC = 106°
IA ⊥ LM, IB ⊥ MN, IC ⊥ NL (радиус ⊥ к касательной)
∢IAM = ∢MBI = ∢IBN = ∢NCI = ∢ICL = ∢LAI = 90°
∢L= 360°−∢AIC−∢LAI−∢ICL = 360−158−90−90 = 360−180−158 =180(2-1)-158=180-158 = 22° (из 4-угольника AICL)
аналогично для других углов:
∢ M= 180−96 = 84°
∢ N= 180−106 = 74°
∢L= 22°∢M = 84°∢N = 74°∪CA = 158°
На ребрах AB и CB треугольной пирамиды DABC отмечены точки М и N, AM:MB=CN:NB=3:1. P и Q - середины ребер DA и DC. В каком отношении плоскость PQM делит пирамиду?
PQ||AC, MN||AC (по т о пропорциональных отрезках) => PQ||MN
Через две параллельные проходит плоскость PQMN
Рассмотрим пирамиду с основанием AMNC и вершиной P.
△MBN~△ABC, k=MB/AB=1/4
S(MBN)/S(ABC) =k^2 =1/16 => S(AMNC)/S(ABC) =15/16
Высоты из P и D на (ABC) относятся 1:2
V(PAMNC)/V(DABC) =15/16 *1/2 =15/32
Рассмотрим пирамиду с основанием QNC и вершиной P.
S(QNC)/S(DBC) =CQ*CN/CD*CB =CQ/CD *CN/CB =1/2 *3/4 =3/8
Высоты из P и A на (DBC) относятся 1:2
V(PQNC)/V(ADBC) =3/8 *1/2 =3/16
V(PAMNC)+V(PQNC) =(15/32 +3/16) V(DABC) =21/32 V(DABC)
Плоскость PQM делит пирамиду DABC в отношении 11:21.
Большая часть 21/32 от объема DABC.