Вписанный угол ACB равен 42. Найди соответствующий ему центральный угол АОВ.

👇

Увидеть ответ

Ответ:

antipingv2004

29.01.2022

Объяснение:

Если ACB равен 42, значит градусная мера дуги AB будет 2*42=84°

Мы знаем что центральный угол равен градусной мере дуги, значит AOB=84°

4,8(73 оценок)

Ответ:

оля1890

29.01.2022

***

пусть:

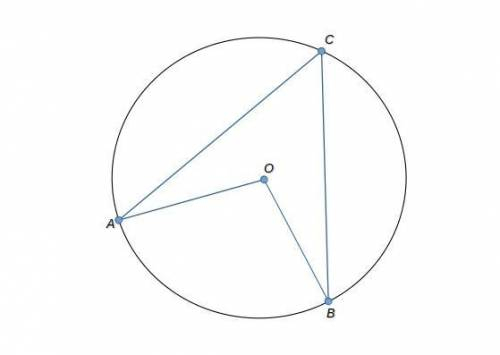
О - центр окружности.

∠АСВ - вписанный угол, который равен 42°

∠АОВ - центральный угол, - неизвестный.

центральный угол - это угол, вершина которого находится в центре окружностивписанный угол - это угол, вершина которого лежит на окружности, а стороны пересекают еевписанный угол равен половине соответствующего центрального угла

следовательно:

∠AOB = 2∠ACB = 2 · 42° = 84°

ответ: центральный угол АОВ равен 84°

4,7(98 оценок)

Открыть все ответы

Ответ:

puzhalina77Frik

29.01.2022

Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.

В прямоугольном треугольнике катету противолежит острый угол ( прямой противолежит гипотенузе) и сумма острых углов 180°-90°=90°.

Поэтому: если противолежащий катету острый угол одного прямоугольного треугольника равен противолежащем острому углу другого, то прилежащие к равным катетам острые углы также равны

К равным катетам этих треугольников прилежат равные углы: прямой ( по условию) и найденный острый.

Такие прямоугольные треугольники равны по 2-му признаку равенства треугольников, т.е. по стороне и прилежащим к ней углам.

4,8(37 оценок)

Ответ:

Market080808

29.01.2022

Подобие треугольников --- это "про равные углы"...
в треугольнике АВС больший угол (против большей стороны) ∠АВС
в ΔКАС самая длинная сторона (против большего угла)-- сторона КС
в любом случае КС пропорциональна АС: KC = k*AC = 10k
вторая сторона ΔКАС АС=10
осталось определиться с третьей стороной (АК)
возможны два варианта:
АК > AC или AK < AC
1) AK > 10
тогда АС самая короткая сторона ΔКАС и она пропорциональна ВС
АС = k*BC ---> 5k = 10 ---> k = 2
тогда КС = 20, АК = k*9 = 18
по т.косинусов 10² = 20² + 18² - 2*20*18*cos(AKC)
cos(AKC) = (400+324-100) / (40*18) = 624/(4*6*30) = 26/30 = 13/15
2) AK < 10
тогда АK самая короткая сторона ΔКАС и она пропорциональна ВС
АK = k*BC = 5k, а АС пропорциональна средней стороне АВ
АС = k*АВ ---> k = 10/9
тогда КС = 100/9, АК = 50/9
по т.косинусов 10² = (100/9)² + (50/9)² - 2*100*50*cos(AKC) / 81
100*81 = 100*100 + 25*100 - 100*100*cos(AKC)
cos(AKC) = (100+25-81) / 100 = 44/100 = 0.44
--------------------------------------------------------------------
другими словами, можно было просто посчитать косинусы оставшихся двух углов ΔАВС --- ∠САВ и ∠АСВ, но важно понимать---почему...
а по косинусу ∠АВС (бО'льшего угла треугольника)) и
по т.косинусов можно определить вид треугольника АВС (и КАС)))
10² = 9² + 5² - 2*9*5*cos(ABC)
cos(ABC) = (81+25-100) / 90 = 6/90 = 1/15 > 0 ---> треугольник остроугольный))

Втреугольнике авс ав=9, вс=5, ас=10. точка к расположена вне треугольника авс, кс пересекает ав в то