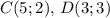 или
или 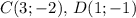
Объяснение:
Расстояние между двумя точками 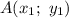 и
и 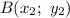 находится по формуле
находится по формуле 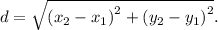
Поэтому
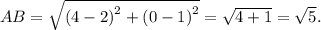
Уравнение прямой, проходящей через точки 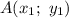 и
и 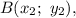 имеет вид
имеет вид
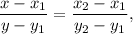
поэтому уравнение прямой 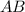
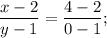
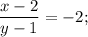
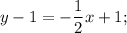
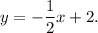
Угловой коэффициент найденной прямой 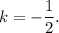
Так как стороны квадрата перпендикулярны, уравнения прямых, которые их выражают, должны удовлетворять условию перпендикулярности с заданной прямой (для перпендикулярных прямых с угловыми коэффициентами 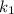 и
и 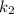 выполняется равенство
выполняется равенство 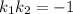 ).
).
Тогда угловой коэффициент прямых, проходящих перпендикулярно отрезку 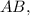 равен
равен 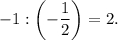
Значит все такие прямые имеют вид 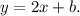
Подставив координаты точки 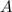 в полученное уравнение, найдем
в полученное уравнение, найдем
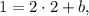
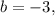
Значит уравнение прямой, перпендикулярной 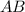 и проходящей через точку
и проходящей через точку 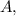
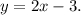
Аналогично подставив координаты точки 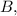 получим
получим
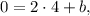
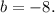
Значит уравнение прямой, перпендикулярной 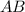 и проходящей через точку
и проходящей через точку 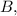
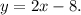
Таким образом, точка 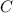 лежит на прямой
лежит на прямой 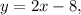 т. е. ее координаты
т. е. ее координаты 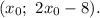 А длина стороны
А длина стороны 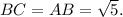
Пользуясь формулой расстояния между двумя точками (см. выше), получаем:
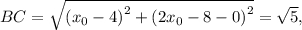
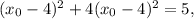
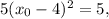
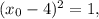
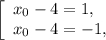
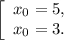
Вычисляем соответствующие значения y для этих точек: для 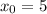
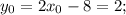 для
для 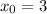

Выходит, два возможных положения точки C — 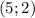 или
или 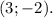
Проделываем ту же последовательность действий для определения координат точки 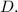 Так как она лежит на прямой
Так как она лежит на прямой 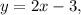 то
то 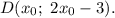
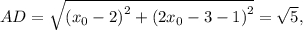
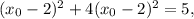
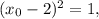
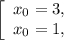
тогда для 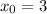
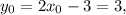 а для
а для 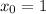
 Значит возможные положения точки
Значит возможные положения точки 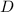 —
— 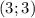 или
или 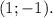
1)Сначала рассмотрим треугольники АВО и СОМ
АО = ОС - по условию
ВО = ОМ - по условию
угол ВОА = угол МОС - вертикальные, следовательно треугольники равны по первому признаку равенства треугольников, следовательно АВ = СМ и угол АВО = углу СМО
2)Затем рассмотрим треугольники ВОС и АОМ
ВО = ОМ - по условию
ОС = ОА - поу словию
угол ВОС = углу АОМ - вертикальные, следовательно треугольники равны по первому признаку равенства треугольников, следовательно ВС = АМ и угол АМО = угол ОВС
3) угол АВС = угол АВО + угол ОВС
угол АМС = угол АМО + угол ОМС
угол АМО = угол ОВС
угол АВО = углу СМО, следовательно угол АВС = углу АМС
4)Рассмотрим треугольники АВС и АМС
АВ = СМ - по доказонному (1)
ВС = АМ - по доказонному (2)
угол АВС = углу АМС - по доказонному (3), следовательно треугольники равны по первому признаку равенства треугольников
Задача имеет два решения:
1) С(5;2), Д(3;3)
2) С(3;-2), Д(1;-1)