За теоремою синусів
с²=а²+в²-2ав×cosα, де а=8 см в=7 см α=60°
с - третя невідома сторона
с²=8²+7²-2×8×7×cos60°
с²=64+49-112×0,5
с²=113-56
с²=57
с=7,5 (см)
Відповідь: 7,5 см третя сторона трикутника.
3)11
Объяснение:
АВСДА1В1С1Д1 - усеченная пирамида , в основаниях квадраты АВСД со стороной =10, А1В1С1Д1 со стороной=2, ОО1-высота пирамиды=7, АС=корень(АД в квадрате+СД в квадрате)=корень(100+100)=10*корень2, А1С1=корень(А1Д1 в квадрате+С1Д1 в квадрате)=корень(4+4)=2*корень2,
рассматриваем АА1С1С как равнобокую трапецию, АА1=СС1, проводим высоты А1К и С1Н на АС, КА1С1С-прямоугольник А1С1=КН=2*корень2, А1К=С1Н=ОО1=7-высота, треугольник АА1К=треугольник НС1С как прямоугольные по гипотенузе и катету, АК=СН=(АС-КН)/2=(10*корень2-2*корень2)/2=4*корень2
АН=АК+КН=4*корень2+2*корень2=6*корень2, треугольник АС1Н прямоугольный, АС1-диагональ пирамиды=корень(АН в квадрате+С1Н в квадрате)=корень(72+49)=11
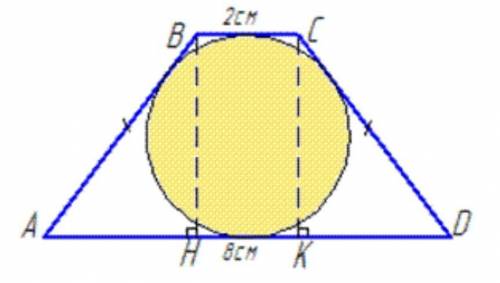
Нехай маємо рівнобічну трапецію ABCD, AD||BC, BC=2 см, AD=8 см, AB=CD, BH⊥AD, де BH– висота трапеції, опущена на сторону AD.
Оскільки у рівнобічну трапецію ABCD вписане коло, то суми її протилежних сторін рівні (за властивістю чотирикутника, описаного навколо кола), тобто AB+CD=AD+BC, звідси
2AB=8+2=10, AB=AD=10/2=5 см.
Опустимо ще одну висоту CK на сторону AD, тобто CK⊥AD (∠CKD=90).
Розглянемо прямокутні трикутники ABH і KCD.
У них ∠BAH=∠CKD – як кути при основі AD у рівнобічній трапеції ABCD (за властивістю), і CD=AB=5 см.
Тому, за ознакою рівності прямокутних трикутників, трикутники ABH і KCD рівні (за гіпотенузою і гострим кутом), і, отже, AH=KD=(8-2)/2=3 см.
≈5 см
Объяснение:
Дано: ΔАВС, АС=8 см, ВС=7 см, ∠А=60°. АВ - ?
Знайдемо ∠В за теоремою синусів:
Sin60/7 = sinB/8
sinB=8*sin60:7=8√3/7*2=4√3/7≈0,9897.
∠В≈81°
∠С=180-60-81≈39°
Знайдемо АВ за теоремою косинусів:
АВ²=АС²+ВС²-2*АС*ВС*соs39°=64+49-112*0,7771=113-87≈26
АВ≈5 см.