Question

У трикутник зі стороною 10 см і висотою 7 см, проведеною, до даної сторони, вписано прямокутник, сторони якого відносяться як 4:7,
причому менша сторона прямокутника належить даній стороні
трикутника. Знайдіть сторони прямокутника.

Answer 1

Стороны прямоугольника равны 5 и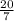 $\frac{{20}}{7}$

Объяснение:

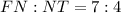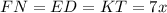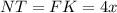Пусть $FN:NT = 7:4$; $FN = ED = KT = 7x$, $NT = FK = 4x$.

Так как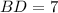 $BD = 7$, то $BE = 7 - 7x$.

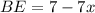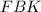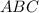Треугольники $FBK$ и $ABC$ подобны, поэтому

$\displaystyle\frac{{BE}}{{BD}} = \displaystyle\frac{{FK}}{{AC}};displaystyle\frac{{7 - 7x}}{7} = \displaystyle\frac{{4x}}{{10}};1 - x = \displaystyle\frac{{2x}}{5};5 - 5x = 2x;7x = 5;x = \displaystyle\frac{5}{7}.$

Тогда

$FN = 7x = 7 \cdot \displaystyle\frac{5}{7} = 5;$

$FK = 4 \cdot \displaystyle\frac{5}{7} = \displaystyle\frac{{20}}{7}.$