ответ: 4*x+10*y-85=0.
Объяснение:
Для того, чтобы все точки прямой a*x+b*y+c=0 находились на равных расстояниях от точек А и В, эта прямая должна быть перпендикулярна прямой АВ и проходить через середину отрезка АВ. Пусть x1 и y1 - координаты точки А, а x2 и y2 - координаты точки В; составим уравнение прямой АВ:
(x-x1)/(x2-x1)=(y-y1)/(y2-y1), (x-4)/(6-4)=(y-4)/(9-4), (x-4)/2=(y-4)/5, y=5/2*x-6. Отсюда следует, что угловой коэффициент этой прямой k1=5/2. А так как прямая a*x+b*y+c=0 перпендикулярна прямой АВ, то её угловой коэффициент k2=-1/k1=-2/5. Пусть точка С - середина отрезка АВ; найдём её координаты x3 и y3:
x3=(x1+x2)/2=5, y3=(y1+y2)/2=13/2. Теперь составляем уравнение прямой a*x+b*y+c=0: y-y3=k2*(x-x3), y-13/2=-2/5*(x-5), 4*x+10*y-85=0.
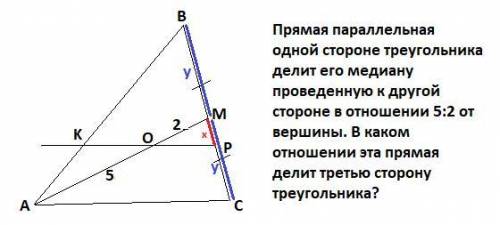
Прямая параллельная одной стороне треугольника делит его медиану проведенную к другой стороне в отношении 5:2 от вершины. В каком отношении эта прямая делит третью сторону треугольника?
Объяснение:
Введем обозначения как показано на чертеже: КР║АС , ВМ=МС=у, МР=х . По условию 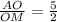 . Необходимо найти
. Необходимо найти 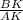 .
.
Т.к. АС║КР , то по т. о пропорциональных отрезках 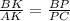 или
или
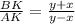 (*) . По т. Менелая для ΔВАМ :
(*) . По т. Менелая для ΔВАМ :
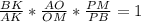 или
или 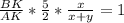 или
или 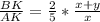 (**).
(**).
Приравняем правые части (*) и (**) : 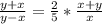 или 2(у-х)=5х или
или 2(у-х)=5х или
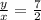 .
.
Вернемся к (**) 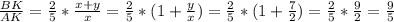 .
.
а)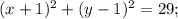
б)
Объяснение:
Если точки и
и  являются концами отрезка, то его серединой будет точка
являются концами отрезка, то его серединой будет точка
Эта точка и будет являться центром окружности, а расстояние до любого из концов отрезка — радиусом.
Расстояние между точками и
и  находим по формуле
находим по формуле
Зная центр окружности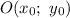 и ее радиус
и ее радиус  , записываем уравнение
, записываем уравнение
а)
б)