Дано:
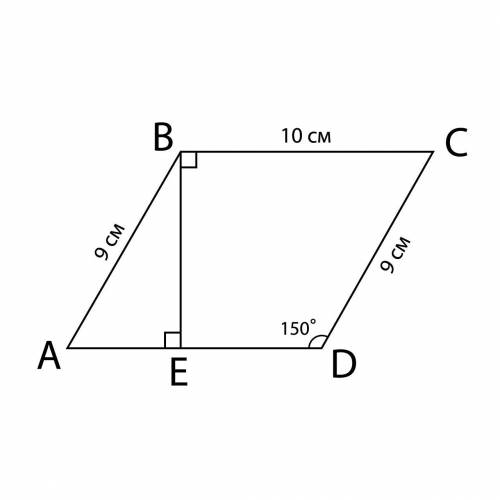
ABCD - параллелограмм.
∠ABC = ∠ADC = 150°
AB = CD = 9 см
BC = AD = 10 см
Найти: S параллелограмма ABCD
∠BAD = ∠BCD = (360° - ∠ABC - ∠ADC) ÷ 2 =
= (360° - 150° - 150°) ÷ 2 = 60° ÷ 2 = 30° (сумма углов параллелограмма равна 360°)
Опустим высоту BE
Рассмотрим прямоугольный треугольник ABE:
∠A = 30° ⇒ BE = 1/2AB = 4,5 см (в прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы)
S параллелограмма ABCD = AD × BE = 10 × 4,5 = 45 см² (площадь параллелограмма равна произведению его стороны на высоту опущенную к этой стороне)
ответ: 45 см²
№2Рассмотрим треугольник CDE:
∠C = 180° - ∠D - ∠E =
= 180° - 45° - 90° = 45° (сумма углов треугольника равна 180°)
∠C = ∠D ⇒ ΔCDE равнобедренный ⇒
⇒ CE = DE = 4 см
Рассмотрим прямоугольный треугольник CBF:
∠B = 180° - 90° - 60° = 30° (сумма углов треугольника равна 180°)
Пусть AF = x
Тогда AB = 2x (в прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы)
Найдём x:
x² + 4² = (2x)² (теорема Пифагора)
16 = 4x² - x²
3x² = 16
x² = 16/3
x = 4/√3 = (4√3)/3 см = AF
FE = BC = 3 см
AD = AF + FE + DE = (4√3)/3 + 3 + 4 =
= (4√3)/3 + 7/1 = (4√3 + 21)/3
S трапеции ABCD = (AD + BC)/2 × CE =
= ((4√3 + 21)/3 + 3)/2 × 4 =
= (4√3 + 30)/3 × 2 = (8√3 + 60)/3 (площадь трапеции равна полусумме оснований умноженной на высоту)
ответ: (8√3 + 60)/3
№3 (чертёж прилагается)Дано:
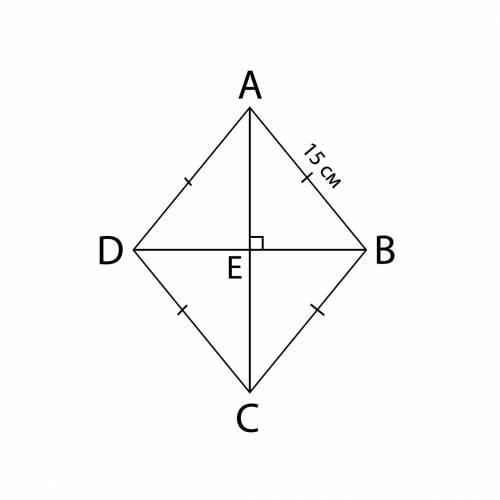
ABCD - ромб со стороной 15 см
AC = 24 см
Найти: S ромба ABCD
Проведём вторую диагональ.
Диагонали ромба делят друг друга пополам ⇒
⇒ AE = CE = 1/2 AC = 24 ÷ 2 = 12 см
Рассмотрим прямоугольный треугольник ABE:
BE = DE = √(AB² - AE²) = √(225 - 144) =
= √81 = 9 см (теорема Пифагора)
BD = BE + DE = 9 + 9 = 18 см
S ромба ABCD = (AC × BD)/2 =
= (24 × 18)/2 = 24 × 9 = 216 см² (площадь ромба равна половине произведения его диагоналей)
ответ: 216 см²
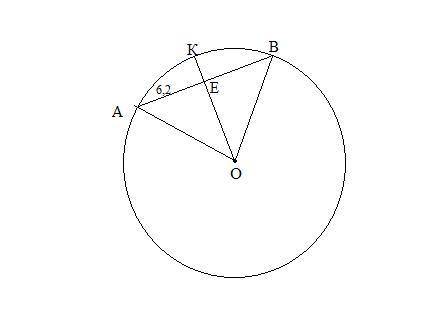
В окружности с центром в точке О проведена хорда АВ, длина которой равна длине радиуса. Перпендикулярно этой хорде проведен радиус ОК. Радиус ОК и хорда В пересекаются в точке Е. Длина отрезка АЕ равна 6,2 см. Нужно а) постройте чертеж по условию задачи; б) найдите длину хорды АВ; в) вычислите длину радиуса; г) найдите периметр треугольника АОВ.
Объяснение:
Δ АОВ-равносторонний ,т.к. АВ=ОВ=ОА.
ОК∩АВ=Е ⇒ ОЕ-медиана ΔОАВ, как высота в равнобедренном треугольнике ⇒ АЕ=ВЕ=6,2 см ⇒ АВ=6,2*2=12,4 см.
ОА=ОВ=ОК=R=12,4 см.
Р(тр)=3*12,4=37,2 (см)
Объяснение:
Щоб знайти відстань від центра кулі до площини трикутника, ми можемо використати теорему Піфагора. Теорема Піфагора говорить, що в прямокутному трикутнику квадрат гіпотенузи рівний сумі квадратів катетів. В нашому випадку, ми знаємо, що радіус кулі складає 5 сантиметрів, і це буде наша гіпотенуза. Також ми знаємо, що сторони трикутника складають 15 сантиметрів і 15 сантиметрів, і це будуть наші катети. Тепер ми можемо розв'язати рівняння, щоб знайти відстань від центра кулі до площини трикутника:
h^2 = 5^2 - (15^2 + 15^2) / 2
h^2 = 25 - 225
h^2 = -200
h =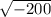
На жаль, коренем з від'ємного числа не може бути, тому ми можемо сказати, що куля не може дотикатися до всіх сторін трикутника. Щоб куля могла дотикатися до всіх сторін трикутника, радіус кулі повинен бути більшим ніж піввисота трикутника.