300 см²
Объяснение:
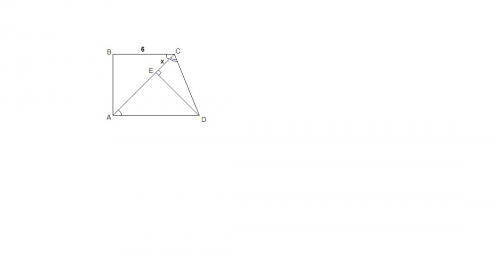
Диагональ трапеции отсекает от нее равнобедренный прямоугольный треугольник, гипотенузой которого является меньшее основание трапеции,а катетами диагональ трапеции и боковая сторона АВ.
Угол трапеции В = 45°.
Из теоремы Пифагора найдём боковую сторону трапеции
с²=а²+в²
а=в, поэтому с²=2а²
20²=2а²
а²=400÷2=200
а=√200=10√2 см
Проведём из угла А высоту к меньшему основанию трапеции.Из полученного прямоугольного ΔАВН находим катет АН=h
AH=a*sinB=10√2sin45°=10√2*√2/2=5*2=10 см
S=(AD+BC)/2 ×AH=(20+40)÷2*10=300 см²
Відповідь:
10; 10; 10*√2
Пояснення:
АВСД - квадрат АВ = ВС = СД = АД = а - сторона квадрата в основании
ВД - диагональ квадрата ВД = а*√2
ДД₁ - выста паралелепипеда
ВДД₁ - прямоугольный треугольник с углами 45 45 90 (равнобедреный)
ВД - катет; ДД₁ - катет; ВД₁=20 - гипотенуза
значит ВД = ДД₁ = ВД₁/√2 = 20/√2 = 10*√2 = а*√2
а = ВД/√2 = 10*√2/√2 = 10