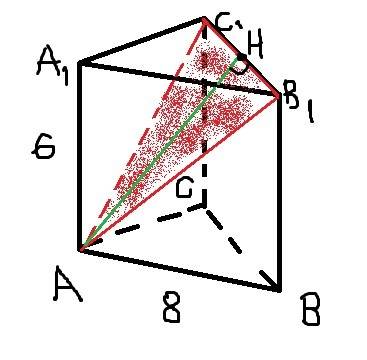
ВСС₁В₁ прямоугольник
ΔАВС - равнобедренный
АВ = АС = √746 ≈ 27,3 см
Объяснение:
Если в четырехугольнике две противоположные стороны параллельны и равны, то это параллелограмм.
Если в параллелограмме есть прямой угол, то это прямоугольник.
ВВ₁ ║ СС₁ как перпендикуляры к одной плоскости,
ВВ₁ = СС₁ = 11 см по условию, значит
ВСС₁В₁ прямоугольник.
ΔАВ₁В = ΔАС₁С по двум катетам (∠АВ₁В = ∠АС₁С = 90°, ВВ₁ = СС₁ и АВ₁ = АС₁), значит АВ = АС, тогда
ΔАВС - равнобедренный.
ΔАВВ₁: ∠АВ₁В = 90°, по теореме Пифагора
АВ = √(АВ₁² + ВВ₁²) = √(25² + 11²) = √(625 + 121) = √746 см
АВ = АС = √746 ≈ 27,3 см
1/2
Объяснение:
Спочатку визначимо значення cos 30° та ctg 45°.
cos 30° = √3/2
ctg 45° = 1
Підставимо ці значення у вираз:
2 cos^2 30° - ctg 45° = 2(√3/2)^2 - 1 = 2(3/4) - 1 = 3/2 - 1 = 1/2
Отже, відповідь: 1/2.