ответ: 1) меньшие по 48°, большие по 132°.
2) меньшие по 40°, большие по 140°
Объяснение: При пересечении двух параллельных прямых секущей образуется пары равных углов:
соответственные (2 и 6, 1 и 5, 3 и 7, 4 и 8).
накрестлежащие: (3 и 5, 4 и 6 - внутренние ), (2 и 8, 1 и 7 - внешние). кроме того, равны и пары вертикальных углов.
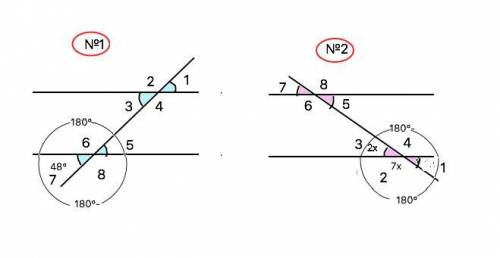
1) Как известно, сумма смежных углов равна 180°. Поэтому углы, смежные углу, равному 48°, равны 180°-48°=132°
На рисунке 1 все мéньшие углы, окрашенные голубым, равны 48°. все бóльшие - 132°
2) На рисунке 2 смежные углы 2 и 3 относятся как 2:7. Т.е. развернутый угол делится на 2+7=9 частей. Каждая часть равна 180°:9=20°. Поэтому все мéньшие углы равны 2•20°=40°, бóльшие 7•20°=140°.
Из условия задачи можно записать:
AB = 2BD
Так как угол B прямой, то треугольник ABD - прямоугольный. Из свойств прямоугольного треугольника, можно записать:
AD^2 + BD^2 = AB^2
Заменим AB на 2BD:
AD^2 + BD^2 = (2BD)^2
AD^2 + BD^2 = 4BD^2
AD^2 = 3BD^2
Также из условия известно, что AS = 12 см. Так как AD является высотой треугольника, то можно записать:
S(ABS) = (ABBD)/2 = (2BDBD)/2 = BD^2
S(ABS) = (ASAD)/2 = (12AD)/2 = 6AD
Таким образом, мы получили два выражения для площади треугольника ABS, которые можно приравнять:
BD^2 = 6AD
Теперь найдем AD:
AD^2 = 3BD^2
AD^2 = 3*(BD^2/2)
AD^2 = (3/2)*BD^2
AD = sqrt((3/2)*BD^2)
AD = BD*sqrt(3/2)
Теперь найдем BD, используя выражение BD^2 = 6AD:
BD^2 = 6AD
BD^2 = 6BDsqrt(3/2)
BD = 6*sqrt(3/2)
Итак, мы нашли BD, теперь найдем AD:
AD = BDsqrt(3/2) = 6sqrt(3/2)sqrt(3/2) = 6sqrt(3/2)^2 = 6*3/2 = 9
Таким образом, AD = 9 см.
черти сам)
Объяснение: