1)
1. E
2. F
3. B
4. E
5. A
6. D.
Теорема косинусов: 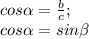
Теорема синусов: 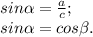
3)
Формула вычисления стороны, зная 2 другие, и угол между ними:
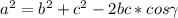
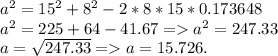
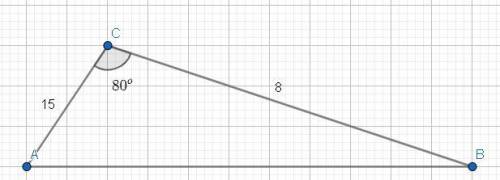
Так как путь из A => B проходит через пункт C, то в этом случае, расстояние между точками A & B равна: AC+BC = 23.
Но так как мы уже нашли 3-ю недостающую сторону(AB(в 1-ой картинке)), то расстояние между точками A => B, без прохода через точку C — равна 23-15,726 = 7.242.
4)
Формула вычисления описанной окружности около равнобёдренного треугольника такова: 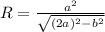
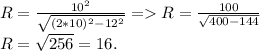
Формула вычисления вписанной окружности около равнобёдренного треугольника такова: 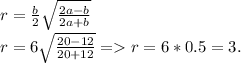
1. Синусы углов пропорциональны сторонам треугольника
Нет такой теоремы.
2. Cтороны треугольника пропорциональны косинусам противоположных им углов
Нет такой теоремы, но выражение присутствует. Это:
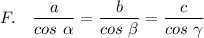
3. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними
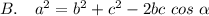
4. Стороны треугольника пропорциональны синусам противоположных им углов
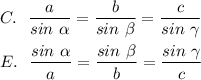
5. Квадрат стороны треугольника равен сумме квадратов двух сторон минус удвоенное произведение этих сторон на синус угла между ними
Нет такой теоремы, но выражение присутствует. Это:
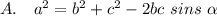
6. Квадрат стороны треугольника равен сумме квадратов двух других сторон плюс удвоенное произведение этих сторон на косинус угла между ними
Нет такой теоремы, но выражение присутствует. Это:
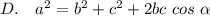
Теорема косинусов 3 (В)
Теорема синусов 4 (C и Е)
МЕ=4 см
Объяснение:
Дві паралельні площини перетинають сторону ВА кута АВС у точках М і М1, а сторону ВС - у точках Е і Е1. Знайти МЕ, якщо ВМ=3см, ВМ1=7,5см, М1Е1=10см.
За умовою задачі маємо кут ABC; площину α, яка перетинає сторони кута ABC у точках М і Е; площину β, яка паралельна площині α і перетинає сторони кута ABC у точках М₁ і Е₁.
Проведемо відрізки МЕ і М₁Е₁.
Оскільки кінці відрізка МЕ належать площині α, то і сам відрізок МЕ належить площині α;
Аналогічно, так як кінці відрізка М₁Е₁ належать площині β, то і сам відрізок М₁Е₁ належить площині β.
За умовою задачі, площини α ║β, тоді МЕ ║ М₁Е₁, за означенням паралельності площин.
Розглянемо ΔМBЕ і ΔМ₁ВЕ₁.
У них:
∠МBЕ=∠ΔМ₁ВЕ₁- як спільний кут при вершині B;∠ВМЕ=∠BМ₁Е₁ - як відповідні кути при паралельних прямих МЕ і М₁Е₁ та січній АВ.Звідси слідує, що за ознакою подібності за двома кутами, трикутники ΔМBЕ і ΔМ₁ВЕ₁ подібні, а значить їх відповідні сторони пропорційні.
Тоді:
За умовою задачі МВ=3 см, М₁В=7,5 см, М₁Е₁=10 см. Звідси, отримаємо:
Відповідь: 4 см
#SPJ1