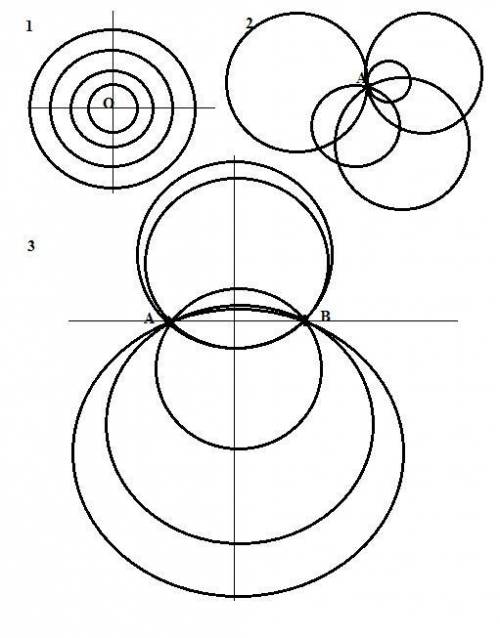
1 - д. 2 - д 3 - д.
Объяснение:
1. Точка может быть центром бесконечного числа концентьрических окружностей (окружностей разных радиусов).
2. Через одну точку можно провести бесконечное число пересекающихся (или касающихся) окружностей.
3. Так как через три точки можно провести единственную окружность, а даны только 2 точки, то третья точка может располагаться в любом месте. Значит через две точки можно провести бесконечное число пересекающихся (имеющих две общие точки) окружностей. Центры этих окружностей будут лежать на серединном перпендикуляре к отрезку АВ.
Для начала, найдем наклон прямой (m). Наклон определяется как изменение координаты y, деленное на изменение координаты x между двумя точками.
Из точек A(-5, 3) и B(2, 4) получаем:
Δy = 4 - 3 = 1 (изменение координаты y)
Δx = 2 - (-5) = 7 (изменение координаты x)
Наклон (m) будет равен Δy/Δx:
m = 1/7
Теперь, используя одну из точек и найденный наклон, можно найти свободный член (b). Подставим координаты точки A(-5, 3) в уравнение прямой и решим его для b:
3 = (1/7)(-5) + b
3 = -5/7 + b
3 + 5/7 = b
21/7 + 5/7 = b
26/7 = b
Таким образом, мы нашли наклон (m = 1/7) и свободный член (b = 26/7) уравнения прямой.
Итак, уравнение прямой, проходящей через точки A(-5, 3) и B(2, 4), имеет вид:
y = (1/7)x + 26/7