ответ: M(3;2) и N(0;4)
Пошаговое решение:
1) По условию отрезок AB должен быть параллелен отрезку MN. Значит, их точки имеют одну общую координату с соответствующей точкой на отрезке, параллельном данному и одну различающуюся.
2) Составим линейную функцию для прямой, которой принадлежат точки A и B. Так как точка A находится ниже точки B, коэффициент линейной функции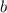 
будет отрицательным: прямая пойдёт вниз по оси Y.
3) Найдём коэффициент линейной функции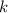 
по формуле:
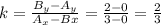
4) Так как точки C, M и N коллинеарны, они принадлежат одной прямой. Это значит, что прямая с точками C, M и N должна вся быть параллельная прямой с точками A и B. Значит, у этих двух прямых будет одинаковый коэффициент наклона .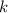
5) Точка M будет находиться над точкой A по оси Y, точка N будет находиться над точкой B по оси Y. Зная координаты точки C и коэффициент наклона 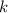, можно рассчитать координаты точек M и N.
6) Рассчитаем координаты точки M:
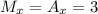
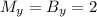
7) Рассчитаем координаты точки N:
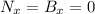
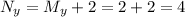
По коэффициенту 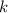доказываемо, что эти координаты справедливы: сдвинувшись на 3 влево по x, получим координату x для точки M, равную 3, а поднявшись на 2 вверх по y, получим координату y для точки M, равную 2. Сдвинувшись на 3 влево по x от точки M, получим координату x для точки N, равную 0, а поднявшись на 2 вверх по y, получим координату y для точки N, равную 4.
Внутренние разносторонние углы при двух параллельных прямых и секущей - это такая пара углов, которая лежит по разные стороны от секущей между двумя параллельными прямыми. Их ещё называют внутренними накрест лежащими углами.
Допустим, у нас есть параллельные прямые AB и CD и секущая MN. При этом точки A и B, как и C и D соответственно, лежат по разные стороны от секущей. Точки M и N лежат на пересечении секущей с прямыми AB и CD соответственно.
Тогда углы AMN и MND будут внутренними накрест лежащими (разносторонними) углами при параллельных прямых AB и CD и секущей MN.
При даній ситуації, коли відомі радіус окружності (r = 13 см), довжина касательної (16 см) і довжина секущої (32 см), ми можемо використати теорему про секущу та секанс.
За теоремою, якщо зовнішня секуща інтерсектує окружність, то добуток віддалень точок перетину від центра дорівнює квадрату довжини секущої.
Позначимо відстань від центра окружності до точки перетину секущої як x. Тоді відстань від центра окружності до точки перетину касательної також буде x, оскільки касательна є перпендикуляром до радіуса, який проведений у точці дотику.
Таким чином, ми можемо записати наше рівняння:
x * (2r + x) = (32)^2
Підставимо відомі значення:
x * (2 * 13 + x) = 32^2
x * (26 + x) = 1024
26x + x^2 = 1024
x^2 + 26x - 1024 = 0
Знайдемо значення x, використовуючи квадратне рівняння:
x = (-b ± √(b^2 - 4ac)) / 2a
Де a = 1, b = 26 і c = -1024.
Підставимо ці значення і розв'яжемо рівняння:
x = (-26 ± √(26^2 - 4 * 1 * -1024)) / (2 * 1)
x = (-26 ± √(676 + 4096)) / 2
x = (-26 ± √4772) / 2
x ≈ (-26 ± 69.14) / 2
x ≈ (-26 + 69.14) / 2 або x ≈ (-26 - 69.14) / 2
x ≈ 43.14 / 2 або x ≈ -95.14 / 2
x ≈ 21.57 або x ≈ -47.57
Оскільки відстань не може бути від'ємною, то відстань, на яку секуща віддалена від центра окружності, становить приблизно 21.57 см.