S = 50 ед².
Объяснение:
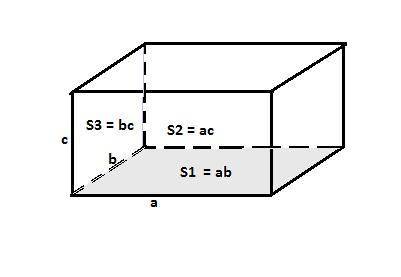
Пусть стороны прямоугольного параллелепипеда, образующие его измерения, равны "a", "b" и "c". Тогда площади основания и двух боковых граней равны
a·b = 48 (1), a·c = 40 (2) и b·c = 30 (3).
Выразим сторону b из равенств (1) и (3) и приравняем полученное:
b = 48/a и b = 30/c => 48/a = 30/c => c = 30a/48 = (5/8)a.
Подставим это значение в (2):
a·(5/8)a = 40 => a² = 320/5 = 64 => a = 8 ед.
Тогда из (1) b = 48/8 = 6 ед. c = 30/8 = 5 ед. (из 2).
Найдем по Пифагору диагональ основания:
d = √(a²+b²) = √(64+36) = 10 ед.
Площадь диагонального сечения равна:
S = d·c = 10·5 = 50 ед².

Проте, ми можемо знайти площу бічної поверхні циліндра. Площа бічної поверхні циліндра розраховується за формулою: S = 2πrh, де r - радіус циліндра, h - висота циліндра.
У даному випадку, переріз циліндра є дугою, яка відсікається від основи по 90°. Тобто, площа цього перерізу буде складати 1/4 від повної площі кола радіусом r. За даними, площа перерізу дорівнює 120 см².
1/4 * π * r² = 120
Щоб розв'язати це рівняння і знайти значення радіуса (r), потрібно поділити обидві частини рівняння на (1/4 * π):
r² = 120 / (1/4 * π)
r² = 480 / π
Таким чином, радіус циліндра (r) дорівнює кореню квадратному з (480 / π).
Отже, ми не можемо точно визначити об'єм циліндра без додаткової інформації про його висоту, але ми можемо знайти радіус і площу бічної поверхні циліндра.