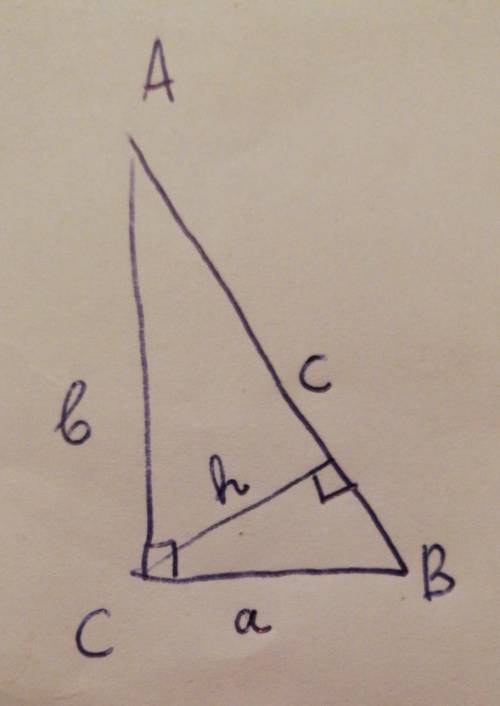
r=5см
Объяснение:
Дано:
а=15см
в=20см
r=?
По теореме Пифагора вычис-
лим гипотенузу треугольника:
с=(20^2+15^2)^1/2=25(см)
Точка пересечения биссектрис
треугольника является центром
его вписанной окружности.
Окружность, вписанная в треу
гольник, касается каждой его
стороны. С другой стороны, ка
сательная перпендикулярна
радиусу, проведенному через
точку касания.
Вывод: расстояние от точки
пересечения биссекрис до ги
потенузы есть радус окруж-
ности, вписанной в этот прямо
угольный треугольник.
Используем формулу радиуса
окружности, вписанной в пря-
моугольный треугольник:
r=а+в-с/2
r=15+20-25/2=10/2=5(см)
расстояние от точки
пересечения биссектрис
до гипотенузы 5см.
АМ дорівнює 8√2 сантиметрів.
Объяснение:
Для знаходження відрізка АМ ми можемо скористатися теоремою синусів у трикутнику АВС.
Згідно з теоремою синусів, відношення довжини сторони до синуса протилежного кута є однаковим для всіх кутів трикутника. Тобто:
AB / sin(C) = AC / sin(B) = BC / sin(A)
Ми знаємо значення кутів А та С, а також довжину сторони ВС. Використовуючи цю інформацію, ми можемо знайти довжину сторони AB.
AB / sin(30°) = 8 / sin(45°)
Ми можемо знайти sin(30°) та sin(45°) шляхом використання значень, які ми знаємо:
sin(30°) = 1/2
sin(45°) = √2 / 2
Тепер можемо підставити ці значення у рівняння:
AB / (1/2) = 8 / (√2 / 2)
Перетворимо рівняння:
AB = (8 * 2) / (√2)
AB = 16 / (√2)
AB = (16 * √2) / 2
AB = 8√2