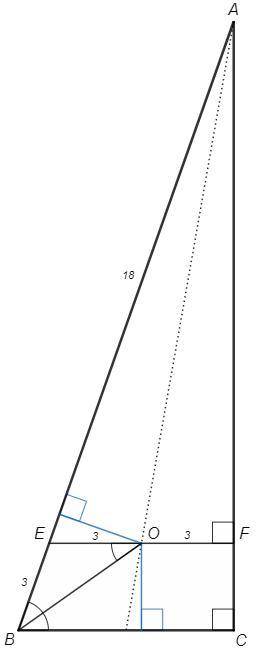
Через точку O проведем EF||BC.
В трапеции пересечение продолжений боковых сторон и середины оснований лежат на одной прямой. О - середина EF.
EO=OF=3, EF=6
Биссектриса внутреннего угла при параллельных отсекает равнобедренный треугольник (∠EOB=∠CBO, накрест лежащие. ∠EOB=∠EBO).
BE=EO=3, AE=18
△ABC~△AEF (по соответственным углам при BC||EF)
BC/EF=AB/AE =21/18 =7/6, BC=7
AC=√(21^2 -7^2) =√(14*28) =14√2
Точка О лежит на биссектрисе угла ABC, следовательно равноудалена от сторон угла. Расстояние между параллельными постоянно, поэтому достаточно найти FC.
AF/AC =6/7 => FC=AC-AF =AC/7 =2√2

Объяснение:
3.
∆ABC - равносторонний
АС=2•DC=2•5√3=10√3
r=(AC•√3)/6=(10√3•√3)/6=5
ответ: 5
4.
сторона квадрата LK=4√6
диагональ квадрата KM=LK√2=4√6√2=
=4√12=8√3
KO=KM/2=8√3/2=4√3
периметр Р=6•АВ
АВ=(2•КО•√3)/3=(2•4√3•√3)/3=
=24/3=8
Р=6•8=48
ответ: 48