1-й признак подобия треугольников (подобие треугольников по двум углам). Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Доказательство.
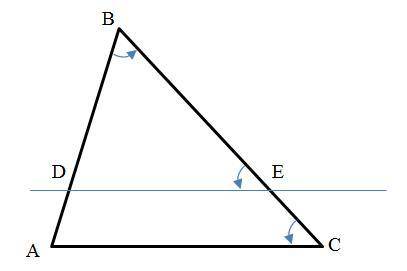
На сторонах AB и BC треугольника ABC отметим точки D и E, соответственно (см. рисунок). Так как ∠BED = ∠BCA, то треугольники ABC и DBE подобны по первому признаку по углам B и ∠BED = ∠BCA.
У подобных треугольников все углы равны, то есть если для треугольников ABC и DBE имеет место ∠B = ∠B и ∠BED = ∠BCA, то ∠BDE = ∠BAC, что требовалось доказать.
Отже, за порівнянням зі стандартною формою, ми бачимо, що центр кола має координати (-1, 2), а радіус кола дорівнює √5.
Объяснение:
Рівняння кола задано у вигляді:
(x + 1)^2 + (y - 2)^2 = 4
Для знаходження координат центра кола, спочатку перетворимо рівняння на стандартну форму (x - h)^2 + (y - k)^2 = r^2, де (h, k) - координати центра кола, а r - радіус кола.
Розкриваємо квадрати:
(x^2 + 2x + 1) + (y^2 - 4y + 4) = 4
x^2 + 2x + y^2 - 4y + 5 = 4
x^2 + 2x + y^2 - 4y + 1 = 0
Для отримання стандартної форми треба віднести константу 1 наліво і завершити квадратичні доданки. Для цього треба додати (2/2)^2 = 1 до лівої та правої частини рівняння:
(x^2 + 2x + 1) + (y^2 - 4y + 4) + 1 = 4 + 1
(x + 1)^2 + (y - 2)^2 = 5
Отже, за порівнянням зі стандартною формою, ми бачимо, що центр кола має координати (-1, 2), а радіус кола дорівнює √5.