(Смотри вложение)
S = 0,5 * BC * AH
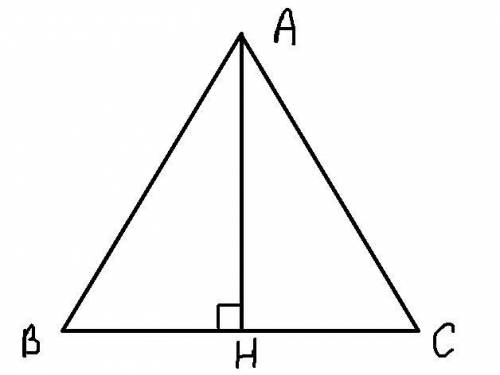
Т.к. ΔABС - равносторонний ⇒ AH является не только высотой, но и биссектрисой и медианой. Из этого можно сделать вывод, что ∠BAH = ∠CAH = 30° и BH=СН
Рассмотрим ΔABH
ΔABH - прямоугольный, т.к. AH -высота
Пусть х - BH, тогда 2х - ВА (т.к. треугольник ΔABС равносторонний и сторона, лежащая напротив ∠ 30° равна половине гипотенузы), тогда по т. Пифагора:
х² + (12√3)² = (2х)²
х² - 4х² + 432 = 0
-3х² = - 432 | : (-3)
х² = 144
x = 12 ( корень -12 мы не берём, т.к. сторона треугольника не может быть отрицательной)
Получается ВС = 2 * ВН = 2*12 = 24
S = 0,5 * 24 * 12√3 = 12 * 12√3 = 144√3 см²
ответ: S = 144√3 см²
Дано:
Сторона паралелограма = 12 см
Друга сторона на 4 см більша = 12 + 4 = 16 см
Висота проведена до меншої сторони = 4 см
Щоб знайти другу висоту, можемо скористатися формулою для обчислення площі паралелограма.
Площа паралелограма дорівнює добутку довжини однієї сторони на висоту, тобто:
Площа = сторона * висота
Ми знаємо, що площа паралелограма може бути також обчислена як добуток довжини іншої сторони на другу висоту. Тому ми можемо записати рівняння:
12 см * 4 см = 16 см * друга висота
Розв'язуємо рівняння для знаходження другої висоти:
48 см² = 16 см * друга висота
Ділимо обидві частини рівняння на 16 см:
друга висота = 48 см² / 16 см
друга висота = 3 см
Отже, друга висота паралелограма дорівнює 3 см.