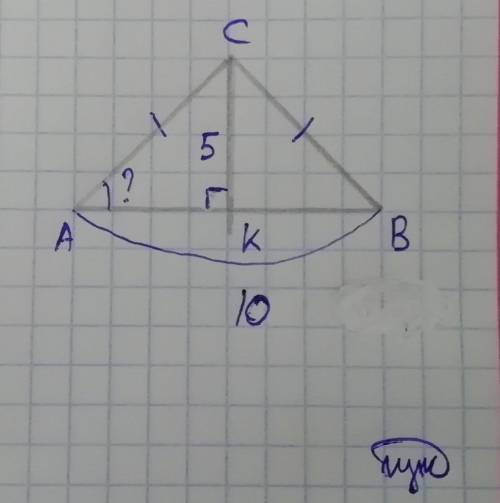
В ΔABC AC = CB ==> ΔABC - равнобедренный
AK = AB/2 = 10/2 = 5 см (биссектриса в равнобедренном треугольнике, проведенная к основанию, есть медиана, т. е. делит основание на две равные части)
Рассмотрим ΔACK
AK = CK = 5 см ==> ΔACK - равнобедренный ==> ∠A = ∠C
∠B = 90° - прямой, поскольку биссектриса в равнобедренном треугольнике, проведенная к основанию, есть высота, т. е. пересекает основание под прямым углом
Пусть ∠A = ∠C = x°. Получим уравнение
x + x + 90 = 180 (сумма углов треугольника равна 180°)
2x + 90 = 180
2x = 180 - 90
2x = 90
x = 90/2 = 45° = ∠A
ответ: ∠A = 45°
1) Поскольку sinα=1/2, значит гипотенуза в 2 раза больше катета. Значит надо построить треугольник с таким отношением.
Если брать конкретные значения, то пусть один из катетов прямоугольного треугольника равен AB=5 см, тогда гипотенуза AC=5*2=10 см.
2) Поскольку sinα=2/5, значит гипотенуза в 5/2=2,5 раза больше катета.
Если брать конкретные значения, то пусть один из катетов прямоугольного треугольника равен AB=4 см, тогда гипотенуза AC=4*2,5=10 см.
3) Поскольку sinα=0,6, значит гипотенуза в 1/0,6=10/6=5/3 раза больше катета.
Если брать конкретные значения, то пусть один из катетов прямоугольного треугольника равен AB=6 см, тогда гипотенуза AC=6*5/3=10 см.
4) sinα=0,7, значит катет в 0,7 раз меньше гипотенузы.
Если брать конкретные значения, то пусть гипотенуза AC=10 см, тогда катет AВ=0,7*10=7 см.