, найденный нами катет является меньшим, поэтому вращение треугольника происходит вокруг него, при этом образуется конус. Осевое сечение конуса представляет собой равнобедренный треугольник, в котором боковые стороны равны образующей, а основание равно диаметру окружности, лежащей в основании конуса, в данном случае образующая равна гипотенузе, диаметр-двум большим катетам данного треугольника, а высота-меньшему катету, значит площадь сечения равна: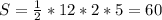
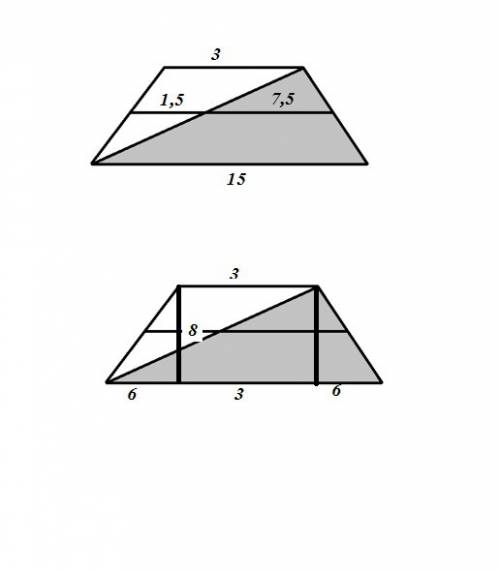
Оскільки точка дотику кола є точкою дотику до вписаного кола, вона лежить на промені, що з'єднує центр кола з центром ромба. Цей промінь є висотою ромба.
За умовою задачі, ця висота розбиває одну сторону ромба на два відрізки довжиною 20 см і 5 см. Оскільки висота розділяє сторону ромба в пропорції 4:1, ми можемо скласти рівняння:
20 см / 5 см = х / (х + h),
де х - довжина коротшого відрізка, h - висота ромба.
Розв'язавши це рівняння, ми знайдемо значення h - висоти ромба.
20 / 5 = х / (х + h)
4 = х / (х + h)
4(х + h) = х
4х + 4h = х
4h = х - 4х
4h = -3х
h = (-3/4)х
Таким чином, висота ромба становить -3/4 від коротшого відрізка. Для того, щоб знайти точне значення висоти, потрібно знати довжину коротшого відрізка або відношення довжин сторін ромба.