Відповідь: фото
Пояснення:
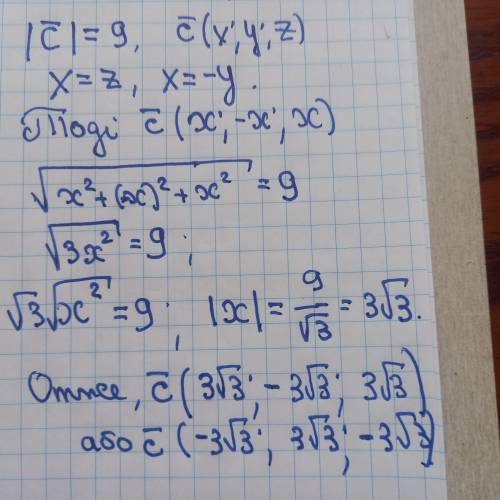
10. Площа трикутника дорівнює добутку радіусу r вписаного кола і полупериметра р.
r=(a+b-c):2 , де а та b - катети, c -гіпотенуза.
a+b=P-с=60-c
r=(60-c-c):2=30-c
Також r=S:p; тоді
S=h*c:2
S=12*c:2=6c
р=60:2=30
r=6c/30=c/5
Отже
c/5=30-c
150-5c=c
6c=150
c=25 см
r=25/5=5 см
S=r*p=5*30=150 см².
Відповідь: 150 см²
12. Нехай дано трикутник АВС - прямокутний, ∠ А - 90°, ВС - гіпотенуза. ВС=32+18=50 см.
АН - висота.
Площа трикутника дорівнює 1\2 * ВС * АН.
АН=√(ВН*СН)=√(32*18)=√576=24 см.
S = 1\2 * 50 * 24 = 600 cм²
Відповідь: 600 см²
6 см
Объяснение:
1) Катет, лежащий против угла 30 градусов, равен половине гипотенузы.
АС - это катет прямоугольного треугольника АСD.
АС лежит против угла 30°, следовательно равен половине АD, которая является большим основанием трапеции:
АС = 24 : 2 = 12 см.
2) Треугольник АВС так же является прямоугольным.
В нём угол В = 90° согласно условию, а угол ВАС равен углу D, так как стороны этих углов взаимно перпендикулярны, а углы со взаимно перпендикулярными сторонами равны.
3) Катет ВС треугольника АВС лежит против угла 30°, следовательно равен половине гипотенузы АС:
ВС = 12 : 2 = 6 см.
4) В трапеции АВСD сторона ВС - это меньшее основание, которое надо было найти. Мы его нашли: ВС = 6см.
ответ: 6 см
Відповідь:
Дано, що модуль вектора c̅ дорівнює 9, тобто ||c̅|| = 9.
Також, за умовою, координати x і z вектора c̅ є рівними, тобто x = z.
Координати x і y є протилежними числами, тобто x = -y.
Ми можемо використати формулу модуля вектора, яка виглядає наступним чином:
||c̅|| = sqrt(x^2 + y^2 + z^2),
де sqrt позначає квадратний корінь.
Підставляючи відомі значення, отримуємо:
9 = sqrt((-y)^2 + y^2 + x^2).
Спрощуючи це рівняння, отримуємо:
9 = sqrt(2y^2 + x^2).
Квадратуючи обидві частини рівняння, отримуємо:
81 = 2y^2 + x^2.
Ми маємо ще дві рівності: x = z і x = -y. Підставляючи ці значення в останнє рівняння, отримуємо:
81 = 2(-y)^2 + (-y)^2.
Спрощуючи це рівняння, отримуємо:
81 = 2y^2 + y^2.
81 = 3y^2.
Ділимо обидві частини рівняння на 3:
27 = y^2.
Звідси випливає, що y = ±√27.
Враховуючи, що x = -y, ми отримуємо:
x = -√27 і x = √27.
Таким чином, координати вектора c̅ будуть:
c̅ (x, y, z) = (-√27, ±√27, -√27) і c̅ (x, y, z) = (√27, ±√27, √27), де ± вказує на два можливих напрямки координати y.
Пояснення: