По теореме о трех перпендикулярах отрезок ОВ - проекция наклонной АВ, перпендикулярной прямой ВС (катеты). Следовательно, двугранный угол АВСО измеряется линейным углом АВО по определению и равен 45° (дано). Треугольник АВО прямоугольный и равнобедренный. Катеты АО=ОВ=2см, а гипотенуза АВ=2√2 см. В прямоугольном треугольнике АВС по Пифагору АС=√(АВ² +ВС²) = √(8+4) = 2√3см. В прямоугольном треугольнике АОС синус угла АСО (искомый угол, так как это угол между наклонной АС и плоскостью α по определению) равен отношению АО/АС = 2/(2√3) = √3/3. По таблице - это угол, равный 35,2°.
ответ: 35,2°.
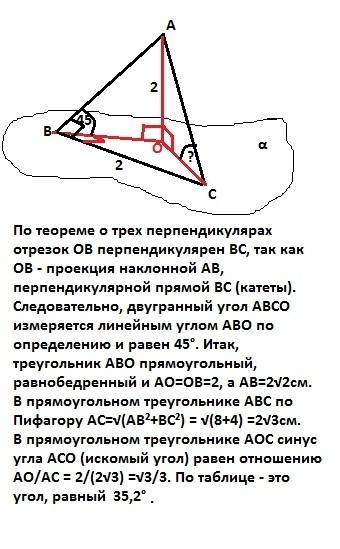
По теореме о трех перпендикулярах отрезок ОВ - проекция наклонной АВ, перпендикулярной прямой ВС (катеты). Следовательно, двугранный угол АВСО измеряется линейным углом АВО по определению и равен 45° (дано). Треугольник АВО прямоугольный и равнобедренный. Катеты АО=ОВ=2см, а гипотенуза АВ=2√2 см. В прямоугольном треугольнике АВС по Пифагору АС=√(АВ² +ВС²) = √(8+4) = 2√3см. В прямоугольном треугольнике АОС синус угла АСО (искомый угол, так как это угол между наклонной АС и плоскостью α по определению) равен отношению АО/АС = 2/(2√3) = √3/3. По таблице - это угол, равный 35,2°.
ответ: 35,2°.

A(-5;-1;-8).
Объяснение:
Как известно, диагонали параллелограмма в точке пересечения делятся пополам. Кроме того, A и C - противоположные вершины параллелограмма. Когда мы сдвигаемся из вершины C в точку O пересечения диагоналей, первая координата уменьшается с -1 до -3, то есть на 2, поэтому при сдвиге из O в A она уменьшится также на 2, то есть превратится в -5. То же рассуждение проведем для второй и третьей координаты. Вторая координата при сдвиге из С в О уменьшилась с 3 до 1, то есть на 2, поэтому при сдвиге в точку А она уменьшится также на 2, то есть превратится в -1. Третья координата при сдвиге из С в О уменьшилась с 4 до -2, то есть на 6, поэтому при сдвиге в точку А она уменьшится также на 6, то есть превратится в -8.