Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис.2).
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1 (см. рис.2). Докажем, что Δ ABC = Δ A1B1C1.
Так как ∠ А = ∠ А1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.
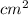
 => 10x+10=60 => 10x=50 => x=5 =>
=> 10x+10=60 => 10x=50 => x=5 =>
За теоремою Піфагора в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. Так як маємо трикутник з прямим кутом D, то можемо скористатись цією теоремою:
AD² = BD² + AB²
Але нам потрібно знайти AD, а не AD². Тож використовуючи операцію взяття квадратного кореня, отримаємо:
AD = √(BD² + AB²)
Тепер застосуємо формули для знаходження значень сторін трикутника SADC (SADC - прямокутний трикутник, бо кут A - прямий):
DC = AB = DN - NC = 4 - 2 = 2 см
NC = BD = 2 см
AD = √(BD² + AB²) = √(2² + 4²) = √20 см
Отже,
DC = 2 см,
NC = 2 см,
AD = √20 см.
Також нам потрібно знайти площу трикутника SADC. Вона розраховується за формулою:
SADC = (AD * DC) / 2
Підставляючи в цю формулу відповідні значення, отримаємо:
SADC = (√20 см * 2 см) / 2 = √20 см² ≈ 4,47 см².
Объяснение: